Para uporządkowana, jest to układ (x,y) dwóch obiektów, w których x jest poprzednikiem pary, a y następnikiem. Oczywiście, mając jakiekolwiek dwa obiekty możemy zawsze utworzyć parę uporządkowaną wskazując, który z nich jest poprzednikiem, a który jest następnikiem. Na przykład, Kubuś Puchatek i jego Pan tworzą znaną parę uporządkowaną (Kubuś, Krzyś).

Parę uporządkowaną należy odróżnić od, po prostu, pary elementów lub zbioru dwuelementowego. {Kubuś, Krzyś} jest dwuelementowym zbiorem, w którym żaden z elementów nie jest w żaden sposób wyróżniony, nie mamy ustalonej kolejności obiektów. W parze uporządkowanej (Kubuś, Krzyś) kolejność jest istotna: Kubuś jest poprzednikiem, a Krzyś następnikiem w tej parze uporządkowanej.

W 1921 roku Kazimierz Kuratowski, podał definicję pary uporządkowanej (x, y) jako zbioru, którego elementami są dwa zbiory: jednoelementowy {x} i dwuelementowy {x, y},

Takie pojęcie pary uporządkowanej jest zgodne z warunkiem równości par uporządkowanych : dwie pary uporządkowane (x,y) i (x', y') są równe, gdy mają równe zarówno poprzedniki jak i następniki

Wynika stąd, że

Z tej definicji wynika, że jeśli jeden ze zbiorów jest pusty, to produkt X × Y też jest zbiorem pustym, bo nie można utworzyć ani jednej pary uporządkowanej. Jeśli natomiast X ma m elementów, a Y n elementów, to można utworzyć nm różnych par.

Pytanie 2.1.1: Czy dla dowolnych zbiorów X × Y = Y × X ?

Przykład 2.1.1

1. Na płaszczyznę Euklidesową przywykliśmy patrzeć jako na zbiór wszystkich punktów postaci (x, y), gdzie x jest odciętą punktu, a y rzędną punktu oraz x ∈ R i y ∈R. Zatem płaszczyzna rzeczywista to po prostu iloczyn kartezjański R × R.
2. Podobnie zbiór liczb zespolonych jest iloczynem R × R. Dowolna liczba zespolona (x + iy) o części rzeczywistej x i części urojonej y, to nic innego jak para uporządkowana o poprzedniku x i następniku y.
3. Jeśli X = {1,2}, a Y = {a,b,c}, to produkt kartezjański X × Y składa się z par uporządkowanych (1,a), (1,b), (1,c), (2,a), (2,b), (2,c).
4. Niech X i Y będą w tym przykładzie przedziałami w zbiorze liczb rzeczywistych, np. X = [3,6], a Y = [2,4]. Wtedy elementy iloczynu kartezjańskiego X × Y wypełniają prostokąt, którego rzutami na osie układu są odpowiednio zbiory X i Y, por. Rys. 2.1.1.

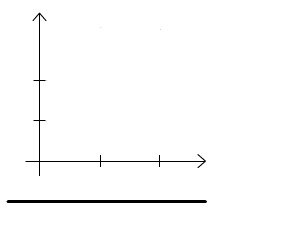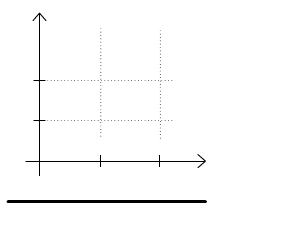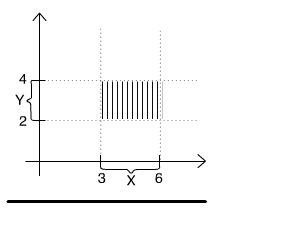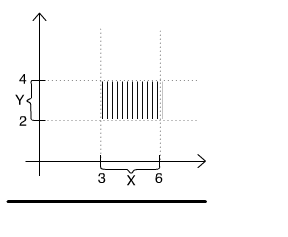
Rys. 2.1.1 Iloczyn kartezjański zbiorów X=[3,6] i Y=[2,4].

W lemacie przedstawionym poniżej zanotujemy związki iloczynu kartezjańskiego z innymi operacjami na zbiorach.

Dowody takich własności najczęściej przeprowadza się pokazując, że uporządkowana para (x, y) należy do lewej strony równości wtedy i tylko wtedy, gdy należy do prawej strony równości. Dla przykładu rozważmy trzecią z równości: (x, y) ∈ X × (A\B) wttw x ∈ X i y ∈ (A \ B) wttw x ∈ X , y ∈ A i y ∉ B wttw : (x, y) ∈ (X × A) i : (x, y) ∉ (X × B) wttw (x, y) ∈ (X × A) \ (X × B).

Nie będziemy tu prezentować dokładnych dowodów pozostałych równości, natomiast posłużymy się ilustracją na płaszczyźnie, by przekonać czytelnika o słuszności drugiej z równości, por Rys. 2.1.2. Niech X będzie pewnym zbiorem zaznaczonym na osi odciętych, a A i B pewnymi podzbiorami zaznaczonymi na osi rzędnych. Lewa strona równości wymaga najpierw wyliczenia przecięcia A ∩ B, co daje w wyniku prostokąt zaznaczony na rysunku 2.1.2a. Prawa strona równości wymaga policzenia osobno iloczynów X × A i X × B, a potem wyliczenia ich przecięcia, por. Rys. 2.1.2b. Otrzymane zbiory są identyczne.

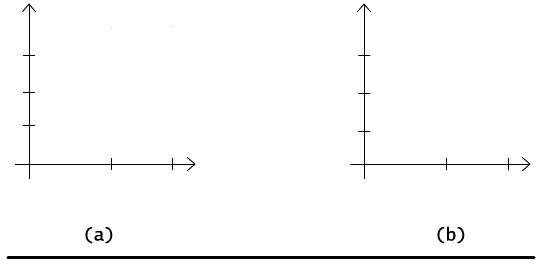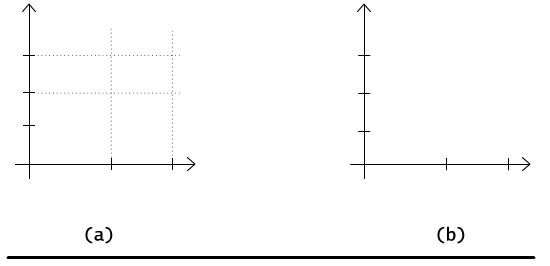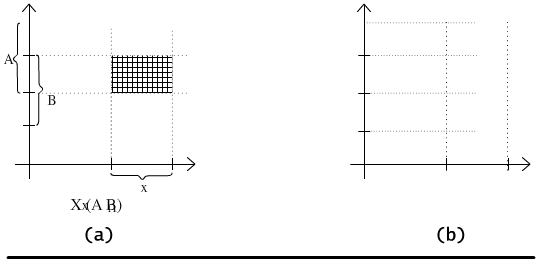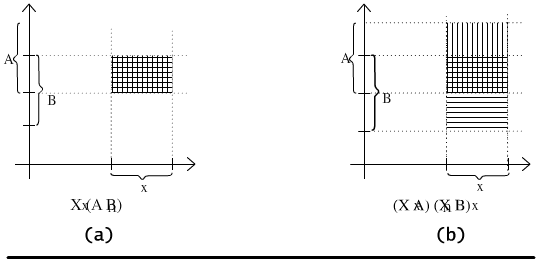
Rys. 2.1.2 Ilustracja graficzna równości X × (A ∩ B) = (X × A) ∩ (X × B).

Zadanie 2.1.1

Udowodnić równość zbiorów X × (A ∪ B) = (X × A) ∪ (X × B).