| « poprzedni punkt | następny punkt » |
Podobnie jak na zbiorach, na relacjach binarnych możemy wykonywać operacje teoriomnogościowe. Jeśli r' i r" są dwiema relacjami binarnymi w X × Y, to r' ∪ r", r' ∩ r", r' \ r" są podzbiorami zbioru X × Y, a więc relacjami dwuczłonowymi w X × Y.
Jeśli do relacji binarnej określonej w produkcie X × Y nie należy żadna para (x,y), to mówimy, że jest to relacja pusta; jeśli natomiast każda para (x,y) dla x ∈ X i y ∈ Y należy do relacji, to mówimy, że jest to relacja pełna.
Pytanie 2.4.1: Jaką relację otrzymamy sumując relacje ≤ i ≥ określone w zbiorze N?
----- Sprawdź odpowiedź -----Pytanie 2.4.2: Jaką relację otrzymamy w wyniku przecięcia relacji ≤ i ≥ określonych w zbiorze N?
Definicja 2.4.1
Niech r będzie relacją binarną w X × Y. Relacją odwrotną do relacji r nazywamy relację r -1 określoną w Y × X taką, że dla dowolnych x ∈ X i y ∈ Y,
(y, x) ∈ r -1 wttw (x, y) ∈ r
Przykład 2.4.1
(1) Relacją odwrotną do relacji ≤ w R jest relacja ≥ w R.
(2) Relacją odwrotną do relacji przedstawionej na rysunku Rys. 2.4.1 (a) jest relacja przedstawiona na rysunku 2.4.1(b).
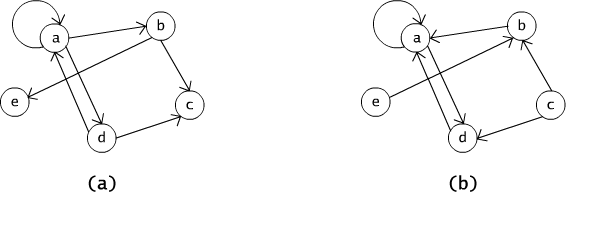
Rys. 2.4.1 (a) Przykład relacji i (b) relacji do niej odwrotnej.
Pytanie 2.4.3: Czy dla dowolnych relacji binarnych r' i r" określonych w X × Y zachodzi (r' ∩ r")-1 = r' -1 ∩ r"-1.
Definicja 2.4.2
Niech r' ⊆ X ×Y oraz r" ⊆ Y × Z. Złożeniem relacji r' z r" nazywamy relację r' ° r" będącą podzbiorem zbioru X ×Z określoną dla dowolnych x ∈ X i z ∈ Z następująco:
(x, z) ∈ r' ° r" wttw istnieje takie y ∈ Y, że (x, y) ∈ r' i (y, z) ∈ r".

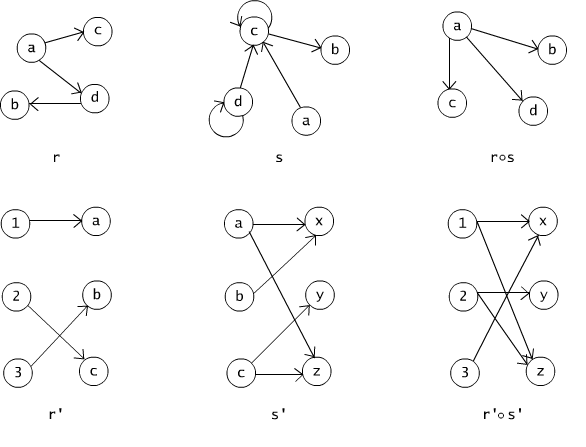
Rys. 2.4.2 Złożenie relacji.
Przykład 2.4.2
Niech r, s, r' i s' będą relacjami przedstawionymi na rysunku 2.4.2a,b. Złożenia r ° s i r' ° s' zostały przedstawione na rysunku 2.4.2c.
Następujący lemat pozwala scharakteryzować w prosty sposób relacje symetryczne i przechodnie przy pomocy wprowadzonych operacji na relacjach.
Lemat 2.4.1
Niech r będzie relacją binarną w zbiorze X. Wtedy
Dowód.
Ad. 1. Jeśli r jest relacją symetryczną i (x, y) ∈ r, to na mocy symetrii (y, x) ∈ r, a stąd (x, y) ∈ r -1. Odwrotnie, jeśli r ⊆ r -1 i (x, y) ∈ r, to (x, y) ∈ r -1, a z definicji operacji odwracania, (y, x) ∈ r. Ponieważ x i y były dowolnymi elementami zbioru X, zatem r jest relacją symetryczną.
Ad. 2. Jeśli r jest relacją przechodnią i (x, y) ∈ r ° r, to na mocy definicji operacji składania, istnieje z takie, że (x, z) ∈ r i (z, y) ∈ r . Stąd i z przechodniości relacji r, (x, y) ∈ r. Zatem r ° r ⊆ r.
Odwrotnie, jeśli r ° r ⊆ r oraz (x, y) ∈ r i (y, z) ∈ r dla pewnych elementów x, y, z zbioru X, to (x, z) ∈ r ° r i w konsekwencji (x, z) ∈ r, co dowodzi przechodniości relacji r.
Pytanie 2.4.4: Czy relacje inkluzji występujące w sformułowaniu powyższego lematu mogą być zastąpione po prostu równością?
Zadanie 2.4.1
Niech r' i r" będą relacjami binarnymi w X. Udowodnić, że
Czy analogiczne twierdzenia można udowodnić dla sumy relacji?
| « poprzedni punkt | następny punkt » |