Rozważmy zbiór studentów PJWSTK. W naturalny sposób możemy wyróżnić dwie grupy : kobiety i mężczyźni. Podzieliliśmy w ten sposób ogół wszystkich studentów na dwie rozłączne klasy. Ponieważ w PJWSTK studiują zarówno dziewczęta jak i chłopcy więc wyróżnione klasy są niepuste. Podobnie, ogół studentów możemy podzielić na grupy w zależności od stopnia zaawansowania studiów: studenci 1-go roku, studenci 2-go roku itd. studenci 5-go roku. Żadna z tych grup nie jest pusta, a w sumie stanowią zespół wszystkich studentów PJWSTK. Matematyczną formalizację pojęcia podziału zbioru przedstawia definicja 5.3.1.

Definicja 5.3.1

Podziałem zbioru X nazywamy indeksowaną rodzinę (X_i)_{i ∈
I} niepustych podzbiorów zbioru X taką, że

Rozważmy jako przykład podział, wyznaczony przez osie układu współrzędnych, określony następująco:

Każdy punkt płaszczyzny należy do dokładnie jednego ze zbiorów podziału, por. Rys. 5.3.1(a).

Inny podział tej samej płaszczyzny stanowią zbiory {(x, y) ∈ R² : x ≥ 0}, {(x, y) ∈ R² : x<0 } zaznaczone na rysunku 5.3.1(b). Przy tym podziale, każdy punkt płaszczyzny należy albo do lewej półpłaszczyzny albo do prawej, w zależności od znaku jego odciętej.

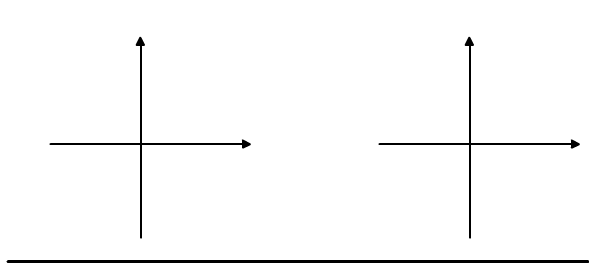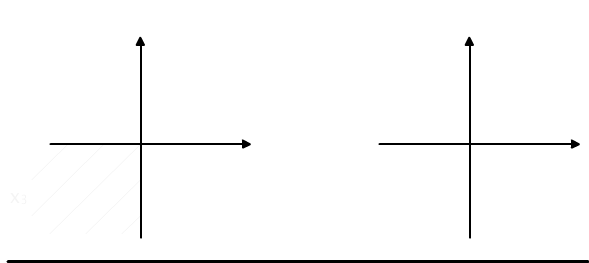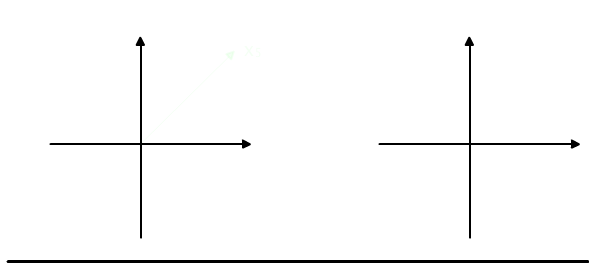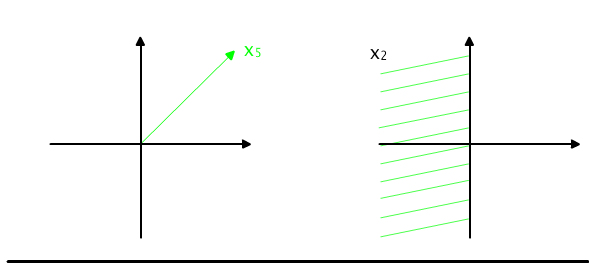
Rys. 5.3.1 (a) Podział płaszczyzny na 5 części. (b) Podział płaszczyzny na 2 części.

Niech K(x) będzie zbiorem punktów okręgu położonego na płaszczyźnie o środku w początku układu współrzędnych i o promieniu x, x ∈ R^≥0. Przyjmijmy dodatkowo, że początek układu współrzędnych jest okręgiem o promieniu 0. Rodzina wszystkich okręgów K(x) dla x ∈ R^≥0 stanowi podział płaszczyzny. Rzeczywiście, każdy z okręgów jest niepusty. Każdy punkt płaszczyzny należy do jakiegoś okręgu (punkt o współrzędnych (x,y) należy do okręgu K( √ (x² +y²)). Ponadto każde dwa zbiory K(x) i K(x'), dla różnych x i x', są rozłączne.

Pytanie 5.3.1: Czy następująca rodzina zbiorów {X₁, X₂, X₃} jest podziałem zbioru liczb naturalnych N?
X₁ = {x ∈ N: x jest kwadratem liczby parzystej k}, X₂ = {x ∈ N: x jest liczbą pierwszą}, X₃ = {x ∈ N: x jest kwadratem liczby nieparzystej}.