| « poprzedni punkt | następny punkt » |
Podobnie jak wszystkie teorie matematyczne, rachunek prawdopodobieństwa wychodzi od pewnych pojęć pierwotnych, które nie są definiowane (por. punkt 8.6). Takim pojęciem w rachunku prawdopodobieństwa jest zdarzenie elementarne. Ogół zdarzeń elementarnych w rozważanym zjawisku (doświadczeniu) nazywamy przestrzenią zdarzeń elementarnych, oznaczamy ją zwykle symbolem Ω. Pojęcie zdarzenia elementarnego i przestrzeni zdarzeń wyjaśnimy na konkretnych przykładach.
Przykład 13.1.1

Rys. 13.1.1 Przestrzeń zdarzeń elementarnych w doświadczeniu polegającym na rzucie kostką sześcienną.
Przykład 13.1.2
Pytanie 13.1.1 Ile elementów zawiera przestrzeń zdarzeń elementarnych w doświadczeniu polegającym na rzucie 3 kostkami sześciennymi do gry?
Zadanie 13.1.1 Określ przestrzeń zdarzeń elementarnych w doświadczeniu polegającym na pokolorowaniu trójpaskowej flagi trzema różnymi kolorami a, b, c.
Odpowiedź: Przestrzeń zdarzeń elementarnych składa się z 6 (=3!)
trójelementowych słów : abc, acb, bac, bca, cab, cba. Każde słowo
określa kolejno kolor pierwszego, drugiego i trzeciego paska.
Definicja 13.1.1
Niech Ω będzie przestrzenią zdarzeń elementarnych. Dowolny podzbiór A przestrzeni zdarzeń elementarnych nazywamy zdarzeniem. Powiemy, że zaszło zdarzenie A, jeśli wynikiem doświadczenia jest zdarzenie elementarne należące do A.
Przykład 13.1.3
W doświadczeniu z rzutem jedną kostką sześcienną (por. przykład 13.1.1(a)) zdarzenia elementarne polegają na wyrzuceniu 1, 2, ... lub 6 oczek, Ω = {1,2,3,4,5,6}.
(a) Zdarzenie A = "wypadła parzysta liczba oczek", to podzbiór trójelementowy {2, 4, 6} przestrzeni Ω.Niech Ω będzie przestrzenią zdarzeń elementarnych, a A zdarzeniem w tej przestrzeni, A ⊆ Ω. Jeśli A = {a1, a2, ..., an}, to zdarzenia elementarne a1, a2, ..., an nazywamy zdarzeniami sprzyjającymi zdarzeniu A.
Powiemy, że zdarzenie A jest pewne, gdy A = Ω, oraz powiemy, że zdarzenie jest niemożliwe, gdy A = ∅.
Uwaga. Nie zawsze jest tak, że przestrzeń zdarzeń elementarnych jest skończona, a zdarzenia są skończonymi podzbiorami tej przestrzeni. W tym wykładzie jednak, będziemy rozważać jedynie przypadek dyskretny, wszystkie rozważane przez nas doświadczenia będą miały skończoną przestrzeń zdarzeń, a wszystkie rozważane zdarzenia tylko skończoną liczbę zdarzeń sprzyjających.
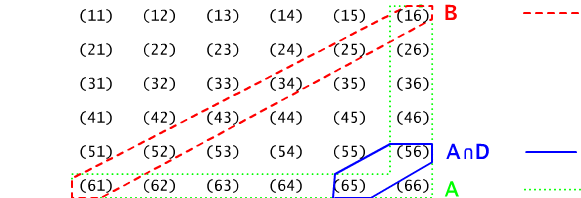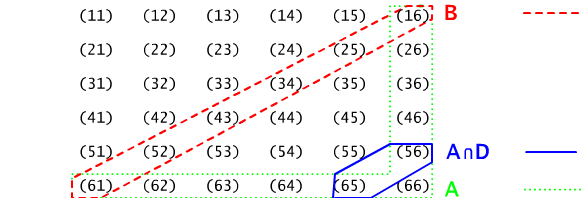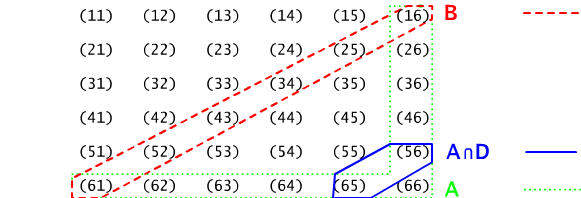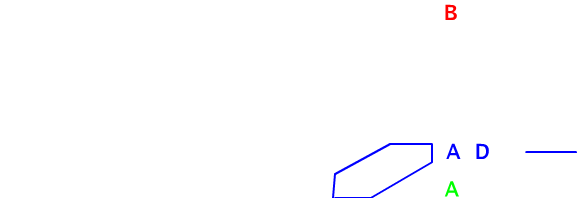
Rys. 13.1.2 Przestrzeń zdarzeń elementarnych w doświadczeniu z rzutem dwoma kostkami sześciennymi. Zaznaczono zdarzenia A=" co najmniej raz szóstka", B= "suma wyrzuconych oczek wynosi 7", oraz przecięcie zdarzeń A i D, gdzie D= "co najmniej raz wypadła piątka".
Przykład 13.1.4
W doświadczeniu polegającym na rzucie dwiema rozróżnialnymi kostkami sześciennymi do gry (np. oznaczonymi jako kostka pierwsza i kostka druga), mamy 36-cio elementową przestrzeń zdarzeń elementarnych Ω = {wij : i, j = 1, 2, ...6}, gdzie, jak łatwo się domyślić, wij jest zdarzeniem elementarnym polegającym na wyrzuceniu na pierwszej kostce i oczek, a na drugiej kostce j oczek, por Rys.13.1.2.
(a) Zdarzenie A = "co najmniej raz wypadła szóstka", to podzbiór przestrzeni zdarzeń elementarnych złożony z wszystkich tych zdarzeń elementarnych, w których na pierwszej kostce wypadła szóstka i tych wszystkich zdarzeń elementarnych, w których na drugiej kostce wypadła szóstka, czyli A = {w6i : i = 1, 2, ...6} ∪ {wi6 : i = 1, 2, ...5, 6}. Jest więc 11 zdarzeń elementarnych w61, w62, w63, w64, w65, w66, w16, w26, w36, w46, w56, sprzyjających zdarzeniu A.Pytanie 13.1.2 Rozważmy doświadczenie z przyklad
13.1.4. Ile zdarzeń elementarnych sprzyja zdarzeniu
"liczba oczek na pierwszej kostce jest dzielnikiem liczby oczek na
drugiej
kostce"?
Na zdarzeniach wykonujemy takie same operacje jak na zbiorach. Nic dziwnego, przecież zdarzenia to zbiory.
Powiemy, że dwa zdarzenia w pewnej przestrzeni zdarzeń elementarnych Ω są identyczne, jeśli mają te same zbiory sprzyjających zdarzeń elementarnych.
W przykładzie 13.1.3 zdarzenia D = "liczba wyrzuconych oczek jest kwadratem liczby naturalnej" i E = "liczba wyrzuconych oczek przystaje do 1 modulo 3 ", chociaż opisywały zdarzenia zupełnie inaczej, są identyczne, bo sprzyjają im dokładnie te same zdarzenia elementarne. W doświadczeniu z rzutem 2 kostkami sześciennymi (por. przykład 13.1.4) zdarzenia C = "iloczyn wyrzuconych oczek jest liczbą parzystą" i zdarzenie "co najmniej na jednej z kostek wypadła liczba parzysta" są zdarzeniami identycznymi, bo dokładnie te same zdarzenia elementarne należą do obu zdarzeń.
Niech A, B będą zdarzeniami, A, B ⊆ Ω . Wówczas zdarzenie A ∪ B nazywamy sumą zdarzeń i zgodnie z definicją sumy teoriomnogościowej zbiorów sprzyjają mu te zdarzenia elementarne, które sprzyjają zdarzeniu A lub sprzyjają zdarzeniu B. Zdarzeniu A ∩ B sprzyjają tylko te zdarzenia elementarne, które sprzyjają zarówno zdarzeniu A jak i zdarzeniu B. Zdarzenie A ∩ B nazywamy iloczynem zdarzeń.
Zdarzenie A' = Ω - A nazywamy zdarzeniem przeciwnym do zdarzenia A. Zdarzeniu A' sprzyjają tylko te zdarzenia elementarne rozważanej przestrzeni, które nie należą do A. Powiemy, że dwa zdarzenia A i B wykluczają się (albo są rozłączne) wtedy i tylko wtedy, gdy A ∩ B = ∅ .
Przykład 13.1.5
Pytanie 13.1.3 Jaka jest moc zbioru zdarzeń elementarnych sprzyjających zdarzeniu "liczba oczek wyrzuconych na pierwszej kostce jest większa niż liczba oczek wyrzuconych na drugiej kostce" w doświadczeniu z rzutem dwiema kostkami sześciennymi do gry?
| « poprzedni punkt | następny punkt » |