| « poprzedni punkt | następny punkt » |
Przykład 15.2.1 Dwuelementowa algebra Boole'a.
Zbiór {true, false} z działaniami
¬ : {true, false} → {true, false}
∨ : {true, false} × {true, false} → {true, false},
∧ : {true, false} × {true, false} → {true, false}
określonymi następująco
¬ true = false, ¬ false = true,
true ∨ a = true i false ∨ a = a dla a ∈ {true, false}
true ∧ a = a i false ∧ a = false dla a ∈ {true, false}
tworzy system algebraiczny B0 = <{true,false}, ¬ , ∨ , ∧ , false,true>. Zwróćmy uwagę, że działania tu przedstawione pokrywają się z operacjami logicznymi, por. punkt 7.2. B0 jest dwuelementową algebrą Boole'a.
Przykład 15.2.2 Algebra zbiorów
Niech X będzie ustalonym zbiorem. Rozważmy zbiór wszystkich jego podzbiorów z operacjami teoriomnogościowymi uzupełnienia w X, sumy i przecięcia zbiorów. System <P(X), -, ∪ , ∩ , ∅ , X > jest algebrą: wyniki wszystkich działań zastosowane do podzbiorów zbioru X dają w wyniku podzbiór zbioru X.
Zwróćmy uwagę, że systemy algebraiczne przedstawione w przykładach 15.2.1 i 15.2.2 są podobne. Każdy z nich ma jedną operację jednoargumentową, dwie operacje dwuargumentowe i dwie stałe. Rzeczywiście sygnatury tych dwóch systemów są takie same.
Przykład 15.2.3 Algebra relacji
Niech U będzie niepustym zbiorem. System <P(U × U), ° , -1, >, którego uniwersum stanowi zbiór wszystkich relacji binarnych w U, a operacjami są operacja składania i operacja odwracania relacji, jest przykładem systemu algebraicznego. Sygnatura tego systemu składa się z dwu operacji: jedna z nich, -1, jest jednoargumentowa, a druga ° jest operacją dwuargumentową. Zarówno operacja składania relacji binarnych jak i operacja odwracania, zastosowane do relacji binarnych w zbiorze U, prowadzą do relacji binarnej w zbiorze U, por. wykład 2.
Pytanie 15.2.1: Czy zbiór wszystkich funkcji ze zbioru X w zbiór X, z operacją składania tworzy algebrę? A zbiór wszystkich funkcji różnowartościowych?
Przykład 15.2.4 Standardowa struktura stosów
Rozważmy niepusty zbiór E i zbiór S ciągów skończonych, których elementy należą do E. Zakładamy, że w zbiorze S znajduje się ciąg pusty oznaczony tu przez 'empty', empty ∈ S. Niech w zbiorze S ∪ E będą określone operacje push, pop, top o sygnaturze
push : S × E →
S
pop : S → S
top : S → E
Dla dowolnego ciągu s = (e1,e2,...,en) i dowolnego elementu e ∈ E, przyjmujemy:
push((e1,e2,...,en), e) = (e1,e2,...,en,e) dla wszystkich n ≥ 0,
pop((e1,e2,...,en)) = (e1,...,en-1) o ile n>0,
top((e1,e2,...,en)) = en o ile n>0.
Operacje pop i top są operacjami częściowymi, bo nie są określone dla elementu 'empty'.
Wtedy <S ∪ E, push, pop, top, empty, = > jest systemem algebraicznym. System ten nazywamy standardową strukturą stosów.
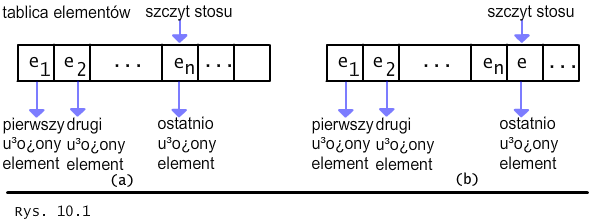
Rys. 15.2.1 (a) Przykładowa realizacja stosu. (b) Wynik włożenia elementu e do stosu opisanego na rysunku (a).
Jeśli Czytelnik słyszał już o strukturze stosów i potrafi ją zaimplementować, to łatwo zobaczy, że każdy zaimplementowany przez niego stos zachowuje się podobnie jak ciągi w naszej strukturze. Operacje dołączania nowego elementu i usuwania elementu wykonuje się tylko na jednym z końców ciągu, zgodnie z zasadą LIFO ("last in first out"). Jeśli Czytelnik jeszcze nie zna struktury stosów, to namawiamy, by zechciał napisać program, który do początkowo pustej tablicy wpisuje nowe elementy i to zawsze na pierwsze wolne miejsce. Zaimplementowanie operacji usuwania ostatnio wpisanego elementu (pop) i operacji sprawdzania jaki element ostatnio został zapisany (top) (mówimy o nim, że znajduje się na szczycie stosu) nie przedstawia żadnych trudności, por. Rys.15.2.1.
Zauważmy, że argumenty operacji push mają różne typy: jednym z argumentów jest ciąg, a drugim element zbioru E. Jest to więc struktura dwusortowa.
Inną strukturą, która zwykle służy do przechowywania skończonych zbiorów jest struktura kolejek. Podobnie jak struktura stosów, jest to system algebraiczny dwusortowy. Dokładną definicje operacji przedstawiamy w następnym przykładzie.
Przykład 15.2.5 Standardowa struktura kolejek
Niech E będzie niepustym zbiorem, a S zbiorem ciągów skończonych o wyrazach należących do E. Zakładamy, tak jak poprzednio, że w zbiorze S znajduje się ciąg pusty oznaczony przez 'empty', empty ∈ S. W zbiorze S ∪ E definiujemy dwuargumentową operację in i dwie jednoargumentowe operacje częściowe out i first o sygnaturze:
in : S × E →
S,
out : S → S,
first : S → E.
Dla dowolnego ciągu (e1,e2,...,en) i dowolnego elementu e ∈ E,
in((e1,e2,...,en), e) = (e1,e2,...,en, e) dla wszystkich n ≥ 0,
out((e1,e2,...,en)) = (e2,...,en), o ile n>0, i nieokreślone w przeciwnym przypadku,
first((e1,e2,...,en)) = e1, o ile n>0 , i nieokreślone w p.p.
System < S ∪ E, in, out, first, empty, => jest przykładem dwusortowego systemu algebraicznego. Nazywamy go standardową strukturą kolejek.
Struktura stosów i struktura kolejek mają taką samą sygnaturę. Są to struktury podobne.
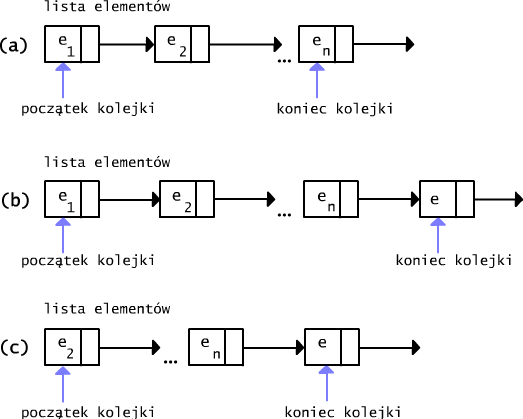
Rys.15.2.2 (a) Przykładowa realizacja kolejki. (b) Wynik włożenia elementu e do kolejki przedstawionej na rysunku (a). (c) Wynik usunięcia elementu z kolejki przedstawionej na rysunku (b).
Zadanie 15.2.1 Napisać algorytmy realizujące operacje w strukturze kolejek, jeśli wiadomo, że kolejka jest reprezentowana przez obiekt, którego atrybutami jest lista dynamiczna elementów kolejki oraz dwa wskaźniki "początek" i "koniec" wskazujące, zgodnie z nazwą, początkowy element kolejki i ostatni element kolejki, por. Rys. 15.2.2.
| « poprzedni punkt | następny punkt » |