Niech będą dwa podobne systemy algebraiczne A = <A, o₁, o₂, ...,o_n, r₁, r₂,... r_m >, B = <B, o'₁, o'₂,..., o'_n, r'₁, r'₂,...,r'_m >, gdzie o_i i o'_i są odpowiadającymi sobie operacjami oraz r_j i r'_j są odpowiadającymi sobie relacjami.

Równości, wymienione w definicji homomorfizmu, określają własność nazywaną zachowywaniem przez homomorfizm operacji i relacji, por. Rys. 15.4.1. Obraz homomorficzny wyniku dowolnej operacji jest identyczny z wynikiem odpowiadającej operacji w drugiej algebrze, zastosowanej do obrazów homomorficznych przyjętych wcześniej argumentów. Podobnie dla relacji. Dany układ argumentów należy do relacji określonej w A tylko wtedy, gdy obrazy homomorficzne tych argumentów należą do odpowiadającej jej relacji w algebrze B.

Rys.15.4.1 Zachowywanie operacji przez homomorfizm.

Przykład 15.4.1

(1) Funkcja h przyporządkowująca podzbiorowi zbioru liczb naturalnych wartość 1 (tzn. wartość prawda) tylko wtedy gdy liczba 1 jest jego elementem, tzn. dla dowolnego zbioru X ⊆ N,

h(X) = 1, gdy 1 ∈ X i h(X) = 0, gdy 1 ∉ X ,

jest homomorfizmem algebry < 2^N, ∪, ∩ , - > w dwuelementową algebrę Boole'a < {0,1}, ∨, ∧, ¬ >.

Rzeczywiście, dla dowolnych zbiorów X i Y będących podzbiorami N,

h(X ∪ Y)=1 wttw 1 ∈ X ∪ Y wttw 1 ∈ X lub 1 ∈ Y wttw h(X) =1 lub h(Y) =1 wttw h(X) ∨ h(Y) = 1. Czyli , h(X ∪ Y)= h(X) ∨ h(Y).

h(X ∩ Y)=1 wttw 1 ∈ X ∩ Y wttw 1 ∈ X i 1 ∈ Y wttw h(X) =1 i h(Y) = 1 wttw h(X) ∧ h(Y) = 1. Czyli , h(X ∩ Y)= h(X) ∧ h(Y).

h(-X)= 1 wttw 1 ∈ -X wttw 1 ∉ X wttw h(X)= 0 wttw ¬ h(X)=1. Czyli , h(-X) = ¬ h(X) .

(2) Niech E będzie zbiorem cyfr {0, 1, 2, 3, ...,9}. Rozważmy dwa podobne systemy algebraiczne: standardową strukturę stosów, por. przykład 15.2.4, <S ∪ E, push, pop, top, empty> i pewną strukturę <N ∪ E, włóż, usuń, pierwszy, 0>, gdzie 0 ∈ E, w których operacje są określone następująco: dla dowolnych e₁, e₂..., e_n, e ∈ E i n ∈ N,

Funkcja h,

h(empty)= 0, h(e) = e dla e ∈E,
 h((e₁,e₂...,e_n)) = włóż(h((e₁,e₂...,e_n-1)),h(e_n))

określona dla dowolnych elementów e₁,e₂...,e_n, e ze zbioru E odwzorowuje zbiór ciągów skończonych S w zbiór liczb naturalnych i ustala homomorfizm między tymi systemami.

Pytanie 15.4.1: Jaką liczbę naturalną przypisuje funkcja h określona w przykładzie 15.4.1(2), stosowi (1,2,5) (stos utworzony przez włożenie kolejno cyfr 1, 2, 5)?

Zadanie 15.4.1 Rozważmy przykład 15.4.1(2). Sprawdź czy zachodzi następująca równość

pierwszy(usuń(włóż(n,e))) = pierwszy(n) ?

Rozwiązanie: Na mocy definicji operacji usuń i włóż mamy:

usuń(włóż(n,e)) = usuń(10(n+1) + e) = (10(n+1) + e)div 10 -1. Ponieważ e<10, więc (10(n+1) + e)div 10 = n+1. Stąd usuń(włóż(n,e)) = n i w konsekwencji pierwszy(usuń(włóż(n,e))) = pierwszy(n).

Przykład 15.4.2

(1) Każdy graf G = <V, E> jest przykładem systemu relacyjnego, z jedną tylko relacją binarną (por. wykład 2). Na rysunku 15.4.2 przedstawiliśmy przykład grafów izomorficznych <G',E'> i <G",E">. Funkcja, która wierzchołkom a, b, c, d, e grafu G' przypisuje odpowiednio wierzchołki 1, 2, 3, 4, 5 grafu G", ustala izomorfizm między tymi grafami. Warunek zachowywania relacji sprowadza się w tym przypadku do równoważności: dla dowolnych wierzchołków x, y grafu G, (x,y) ∈ E' wttw (h(x), h(y)) ∈ E".

(2) Funkcja f(x) = 2x odwzorowująca zbiór liczb naturalnych w zbiór liczb parzystych ustala izomorfizm struktur <N, + > i <P, + >.

Funkcja f jest różnowartościowa i odwzorowuje liczby naturalne na zbiór liczb parzystych, bo, jeśli x ≠ y, to 2x ≠ 2y i jeśli x ∈ P, to x/2 ∈ N oraz f(x/2)=x. Ponadto, f(x+y) = 2(x+y) = 2x + 2y = f(x) + f(y) dla dowolnych liczb naturalnych x i y. Wynika stąd, że f jest izomorfizmem odwzorowującym system algebraiczny <N, + > na system algebraiczny <P, + >.

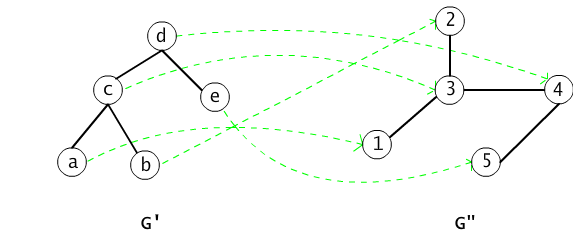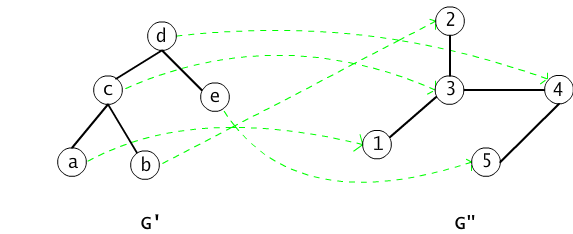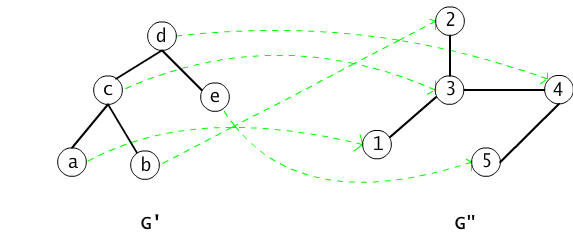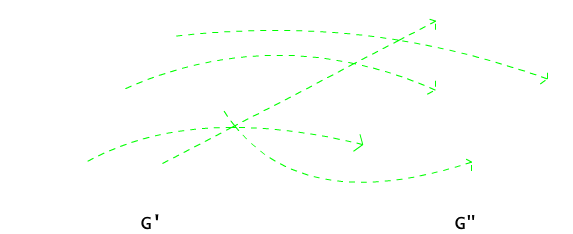
Rys. 15.4.2 Przykład funkcji ustalającej izomorfizm grafów.

Podstawowe własności homomorfizmów i izomorfizmów zebraliśmy w lemacie 15.4.1

Dowód.

Ad. (1) Na mocy definicji składania funkcji (por. definicja 3.4) odwzorowanie (h ° g) przekształca uniwersum systemu A w uniwersum systemu C. Dla dowodu twierdzenia trzeba więc pokazać, że funkcja złożona (h ° g) zachowuje funkcje i relacje. Niech o będzie dowolną operacją n-argumentową w A , a o' i o" odpowiadającymi jej operacjami w systemach B i C. Weźmy dowolny układ argumentów a₁, a₂...,a_n z uniwersum systemu A. Ponieważ funkcje h i g są homomorfizmami zatem

h(o(a₁,a₂...,a_n)) = o'(h(a₁), h(a₂),..., h(a_n)) oraz

g(o'(b₁, b₂,..., b_n))= o"(g(b₁), g(b₂),..., g(b_n)) dla b₁, b₂,..., b_n ∈ B.

Ostatecznie otrzymujemy:

(h ° g) (o(a₁,a₂...,a_n)) = g (h(o(a₁,a₂...,a_n))) = g(o'(h(a₁), h(a₂),..., h(a_n))) = o"(g(h(a₁)), g(h(a₂)),..., g(h(a_n)) ) = o"((h ° g)(a₁), (h ° g)(a₂),..., (h ° g)(a_n)).

Analogicznie rozważmy relację n-członową r w A i jej odpowiedniki r' w B i r" w C. Ponieważ funkcje h i g zachowują relacje to mamy:

r(a₁,a₂...,a_n) wttw r'(h(a₁), h(a₂),..., h(a_n)) dla dowolnych a₁, a₂,..., a_n ∈ A,

r'(b₁, b₂,..., b_n) wttw r"(g(b₁), g(b₂),..., g(b_n)) dla dowolnych b₁, b₂,..., b_n ∈ B.

Stąd

r(a₁,...,a_n) wttw r'(h(a₁),..., h(a_n)) wttw r"(g(h(a₁)),..., g(h(a_n))) wttw r"((h ° g)(a₁),..., (h ° g)(a_n)).

Dowody pozostałych własności pozostawiamy Czytelnikowi jako ćwiczenie. ♦

Ponieważ złożenie dwóch bijekcji jest bijekcją zatem z punktu (1) powyższego twierdzenia wynika następujący wniosek.

Wniosek. Jeżeli h jest izomorfizmem odwzorowującym system A na system algebraiczny B oraz g jest izomorfizmem odwzorowującym system B na system algebraiczny C, to złożenie (h ° g) jest izomorfizmem odwzorowującym system A na system algebraiczny C.

Dowód.

Niech h i g będą dwoma homomorfizmami odwzorowującymi system algebraiczny A w system podobny B. Niech ponadto G będzie zbiorem generatorów systemu A. Na mocy założenia

G ⊆ {a ∈ A: h(a) = g(a)} .

Zbiór {a ∈ A: h(a) = g(a)} jest zamknięty ze względu na wszystkie operacje systemu A. Rzeczywiście, jeśli a₁, a₂,..., a_n ∈ {a ∈ A: h(a) = g(a)}, to dla dowolnej n-argumentowej operacji o w A i odpowiadającej jej operacji o' w B mamy:

h(o(a₁,a₂...,a_n)) = o'(h(a₁), h(a₂),..., h(a_n)) = o'(g(a₁), g(a₂),..., g(a_n)) = g(o(a₁, a₂,...,a_n)).

Wynika stąd, że zbiór {a ∈ A: h(a) = g(a)} jest podalgebrą algebry A. Na mocy definicji 15.3.2, {a ∈ A: h(a) = g(a)} = A, tzn. dla dowolnego a ∈ A, h(a) = g(a), czyli h i g są identycznymi funkcjami. ♦

Twierdzenie, które przedstawiamy na zakończenie rozważań w tym punkcie wykładu jest bardzo ważne. Nosi ono nazwę twierdzenia o izomorfizmie. Jego istotne przesłanie głosi, że systemy izomorficzne są nieodróżnialne przez własności zapisane jako formuły logiki predykatów. W praktyce oznacza to, że jeśli jakiś warunek jest spełniony w systemie A, to będzie też spełniony w każdym systemie z nim izomorficznym.

Zadanie 15.4.2 Udowodnić, że jeśli dwa dowolne skończone grafy są izomorficzne, to sumy rzędów wierzchołków tych grafów są takie same.

Podpowiedź. Trzeba udowodnić, że jeśli a jest wierzchołkiem rzędu k, to jego obraz izomorficzny też musi mieć rząd k.