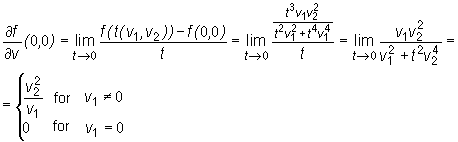2. DIRECTIONAL DERIVATIVE
Definition (directional derivative)
Let f : D → R, D ⊂
Rm, A = (a1,a2,..., am) ∈
IntD and let v = (v1,v2,...,
vm) be a non zero vector. The directional derivative
of f in the direction of vector v is the
limit (if it exists and is finite)
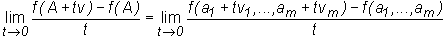
denoted by
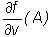 or fv(A).
or fv(A).
Example
Let 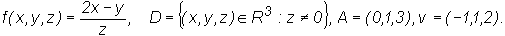
Then

Corollary 1
The partial derivatives of the first order are a specific case of
directional derivatives. Precisely: if ek=(0,...,0,1,0,...,0)
(1 is on the k-th position) is the k-th unit
basis vector Rm, then 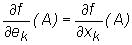 .
.
Because
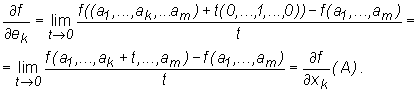
Corollary 2
The existence of all directional derivatives f
at A does not guarantee the continuity of f at the
point A.
Example
Let 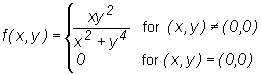 .
.
The function f is not continuous at (0,0),
because

(see the definition of a continuous function).
But for any vector v=(v1,v2) ≠ (0,0) the derivative 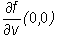 exists,
exists,
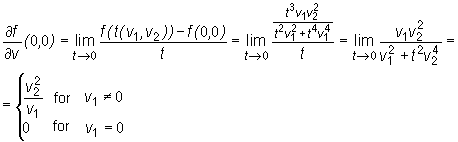
The gradient of a function allows us to easily find the functions
directional derivatives.
Theorem (an expression to find directional derivatives)
Let D ⊂ Rm and
let f : D ⎯→
R be a function which has the following partial
derivatives 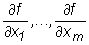 in some neighbourhood of the point A, and which
are continuous at A. Then
in some neighbourhood of the point A, and which
are continuous at A. Then 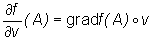 for all non zero vectors v ∈
Rm.
for all non zero vectors v ∈
Rm.
Example
• Find 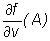 for
for 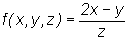 , when A=(0,1,3),
v=(-1,1,2).
, when A=(0,1,3),
v=(-1,1,2).
We know that że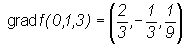 (the first example following the definition of the
gradient). Thus
(the first example following the definition of the
gradient). Thus 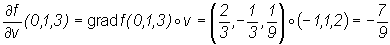 .
.
• Let 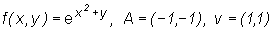 . We find
. We find 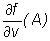 .
.
Then  , thus
, thus 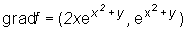 . So
. So
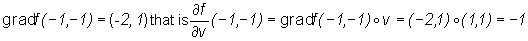 .
.
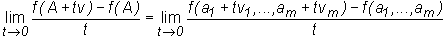
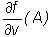 or fv(A).
or fv(A).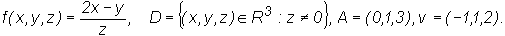

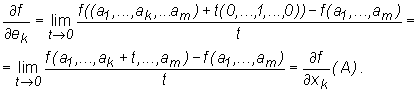
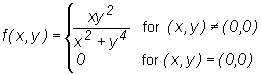 .
.
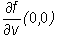 exists,
exists,