Example

We will prove that the series is convergent. This series is an alternating one and

Hence the sequence (a_n) is non increasing and by Leibnitz's test the series is convergent.

Exercise 2.9

Prove that the series is convergent.

Example

The series is convergent by Leibnitz's test. Moreover, the series

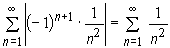
is also convergent, and the series

is absolutely convergent.

Remark

The inverse theorem is not necessarily true.

Example

The series is convergent by Leibnitz's test, but it is not absolutely convergent, because the series with terms | (- 1)ⁿ⁺¹/n | = 1/n, is the harmonic series, and thus it is divergent.

Example

Is the series convergent?

We consider the series

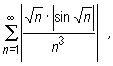
and using the comparison test, we see that for every natural number

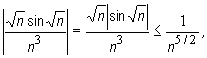
Hence the series is convergent, since the Dirichlet series

is convergent.

Thus the series is absolutely convergent. By the last theorem it is also convergent.

Exercise 2.10

Prove that the series 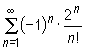is convergent.

Example

We will prove that the series is convergent for every number x.

According to the theorem on the convergence of the absolutely convergent series, our series is convergent if the series

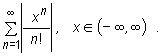
is convergent.

We consider two cases:

• x = 0 ⇒ the series is convergent and the sum is 0.
• Let x ≠ 0. Then

  

  

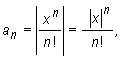
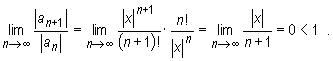
  Hence by the ratio test is convergent.

  Thus the series is absolutely convergent for ,
  which implies that it is convergent for every real number x.

The following theorem illustrates one of the applications of series:

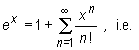
Example

Let x > 0. Using the above theorem we will show that

The number e^x is the sum of the series:

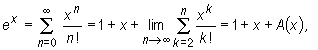
where A(x) > 0, because all elements of the remainder of the 2nd order are positive, provided that x > 0.

Finally we obtain

Exercise 2.11

Is the series convergent?

↔ previous