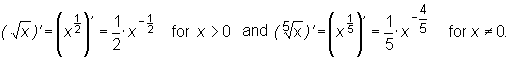
| ↔ previous |
The mentioned below formulae for derivatives of elementary functions should be remembered. They remain valid, provided that both sides are meaningful.
The expression "both sides are meaningful" means for instance:
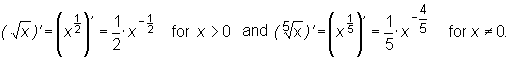
Theorem (the derivative of a compound function)
If functions f and g are differentiable at points x0 and f (x0), respectively, then
| (g · f) ' (x0) = g ' (f (x0)) · f ' (x0). |
Example
Making use of the formulae for derivatives of elementary functions and the last theorem, we will find the derivatives of the following functions:
Using notation of the last theorem we have f (x) = tgx and g (x) = ex. Hence
(g · f) ' (x) = [ g (f (x)) ] ' = (etg x) ' = etg x · (1 / cos²x )
This function is a composition of three functions: f (x) = x1/3, g (x) = cosx and h (x) = sinx, so
y ' (x) = (h · g · f) ' = h ' ( (g · f) (x) ) · (g · f) ' (x) = h ' ( (g · f) (x) ) · g ' (f (x)) · f ' (x) =
= cos (cosx1/3) · (-sinx1/3) · (1/3) x-2/3.
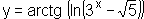
This function is a composition of three functions:
![]()
Hence
y ' (x) = (h · g · f) ' = h ' ( (g · f) (x) ) · (g · f) ' (x) = h ' ( (g · f) (x) ) · g ' (f (x)) · f ' (x) =
![]()
By the last theorem formulae for derivatives of functions f (ax) and f (ax+b) where a,b ∈ R are of the form:
[ ( f (ax) ) ] ' = a f ' (ax)
[ ( f (ax + b) ) ] ' = a f ' (ax + b)
Example
![]()
![]()
Theorem
Let f be a continuous and single-valued function. If f is differentiable at a point x0 and its derivative at this point is different from zero, then a function f -1 is differentiable at a point y0 = f (x0) and:
(f -1) ' (y0) = 1 / f ' (x0). |
Using the last theorem one derives the following formulae:
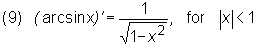


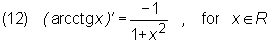
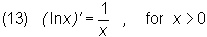
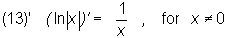
Theorem (the logarithmic derivative)
If a function f is differentiable on an open interval P, f(x) > 0 for x ∈ P, then
| f ' (x) = f (x) · ( ln f (x) ) '. |
Proof
Computing the derivative of lnf (x), making use of the theorem on the derivative of a compound function, we have
(ln f (x) ) ' = ( 1/f (x) ) · f ' (x).
The last theorem is most frequently used for evaluation of derivatives of functions of the form f (x) g(x).
Example
We will find the derivative of the function f (x) = (sinx)x.
We have:
f ' (x) = (sinx)x [ ln (sinx)x ] ' = (sinx)x [ x ln (sinx) ] ' = (sinx)x [ ln( sinx) + x · cosx · (1/sinx) ].
We have made use of the product rule.
| ↔ previous |