Proof. If the function f is constant in the interval [a, b], then f '(x) = 0 for every x∈ (a, b), and thus the claim holds.

Suppose then f is not constant. By the Weierstrass theorem of lecture III there exist points c, c' ∈ [a, b] such that

Since f is not constant, at least one of the inequalities:

holds. Assume that the second inequality is valid (for the first inequality the proof is very similar).

Because f (a) = f (b), then c∈ (a, b). Point c was chosen in such a way that for any h such that c + h ∈ [a, b] we have f (c+h)- f (c) ≤ 0 i.e.

Hence, because f '(c) does exist, by the theorem on inequality preservation of lecture III, we have

0 ≤ f _-' (c) = f' (c) = f ₊' (c) ≤ 0, which implies that f ' (c) = 0.

Example

Let f (x) = cosx, x ∈ [π / 2, 3π / 2]. This function satisfies Rolle's theorem assumptions. Thus there exists a point c∈ [π / 2, 3π / 2] such that f ' (c) = 0. It is plain to see that c = π.

The figure below displays the graph of a function that satisfies Rolle's theorem assumptions:

Fig. 5.1

The tangent to the graph at the point a = (c₂, d) is parallel to the x-axis. It means, that the slope of the tangent is equal 0, i.e., f ' (c₂) = 0.

The mean value theorem is more general than the Rolle's theorem:

If a function f is differentiable in an interval (a, b), then for each secant of its graph there exists a tangent that is parallel to it. This fact becomes clearer, if we notice that the number (f (b) - f (a)) / (b-a) is the slope of the straight line passing through the points (a, f (a)) and (b, f (b)), whereas f ' (c) is the slope of some tangent to the graph of the function f. This is illustrated below.

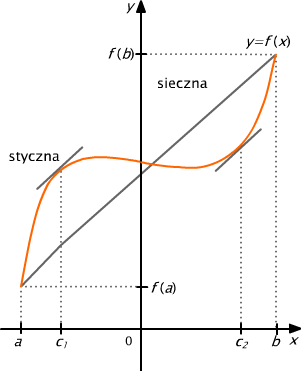
Fig. 5.2

Example

We will use the mean value theorem to prove the inequality

|arctgb - arctga | ≤ |b-a | for a, b ∈ R.

It holds trivially for a = b. We will consider the case a < b (for a > b the proof is similar). The function f(x) = arctgx satisfies the assumptions of the mean value theorem in the interval [a, b]. Transformation of the formula appearing in the theorem gives, for some number c, a < c < b

|arctg b - arctga | = | b-a |·|f ' (c) | = | b-a | · (1/(1+c²)) ≤ |b-a | because 1/ (1+c²) ≤ 1 for c ∈ R.

The following corollaries can be derived from the mean value theorem:

1. If a function f is continuous in an interval P and f ' (x) = 0 for any x ∈ Int P, then f is constant on P.
2. If functions f, g are differentiable in an interval (a, b) and f ' (x) = g ' (x) for every x in this interval, then there exists a number c such that

   f (x) = g (x) + c for every number x ∈ (a, b).

3. Let f, g be functions continuous on an interval P. Now, if for some number x₀ from the interval P the following conditions are satisfied:

   a) f (x₀) ≤ g (x₀)

   b) f ' (x) ≤ g ' (x) for every x ∈ P, x > x₀, then f (x) ≤ g (x) for every x ∈ P, x > x₀.

   If any of the inequalities of assumptions (a) or (b) is strict, the inequality in the claim becomes strict as well.

Example

• We will prove the inequality

arcsinx + arccosx = π / 2 for x∈ [-1, 1].

Consider the function f (x) = arcsinx + arccosx, which is continuous in the interval [-1, 1]. For x ∈ (-1, 1) we have:

Hence f is constant in the interval [-1, 1]. Since f (0) = π / 2, we find that

f (x) = π / 2 for x ∈ [-1, 1].

• We will prove the inequality

sinx < x for x > 0.

Consider the functions f (x) = sinx and g (x) = x, D_f = D_g = R. Let x₀ = 0 and P = [0, 1]. Obviously f (0) = g (0), f ' (x) = cosx ≤ 1 = g ' (x) for x ∈ P, x > 0. Thus by the corollary (3) we obtain sinx ≤ x for x > 0. Since for 0 < x ≤ 1, the inequality f ' (x) = cosx < 1 = g ' (x) holds, for 0 < x ≤ 1 we have sinx < x. The last inequality is clearly valid for x > 1.