↔ previous  next ≈


4. CONVEXITY AND CONCAVITY OF CURVES, INFLECTION POINTS

Definition

We say that a function f is convex in an interval P, if for any numbers x1, x2∈ P and for any number λ, 0 < λ < 1 the following condition is satisfied:

f (λx1 + (1-λ)x2) ≤ λ f (x1) + ( 1-λ) f (x2).

Geometrically, a function f is convex, if each point of a secant segment is located above or at the graph of the function.

Definition

We say that a function f is strictly convex in an interval P, if for any numbers x1, x2∈ P and for any number λ, 0 < λ < 1 the following condition is satisfied:

f (λx1 + (1-λ)x2) < λ f (x1) + ( 1-λ) f (x2).

Geometrically, a function f is strictly convex, if each point of a secant segment connecting the points (x1, f (x1)) and (x2, f (x2)) is located above the graph of the function.

Examples of convex and strictly convex functions are shown in figures 6.1 and 6.2, respectively.

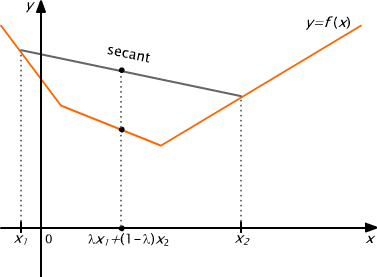
Fig. 6.1

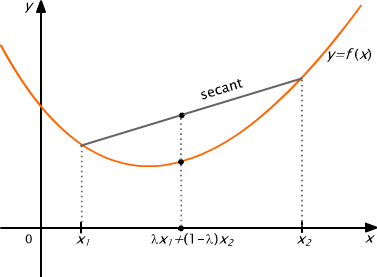
Fig. 6.2

Definition

We say that a function f is concave in an interval P, if for any numbers x1, x2∈ P and for any number λ, 0 < λ < 1 the following condition is satisfied:

f (λx1 + (1-λ)x2) ≥ λ f (x1) + ( 1-λ) f (x2).

Geometrically, a function f is concave, if each point of a secant segment is located below or at the graph of the function.

Definition

We say that a function f is strictly concave in an interval P, if for any numbers x1, x2∈ P and for any number λ, 0 < λ < 1 the following condition is satisfied:

f (λx1 + (1-λ)x2) > λ f(x1) + ( 1-λ) f (x2).

Geometrically, a function f is strictly concave, if each point of a secant segment connecting the points (x1, f (x1)) and (x2, f (x2)) is located below the graph of the function.

Examples of concave and strictly concave functions are shown in figures 6.3 and 6.4, respectively.

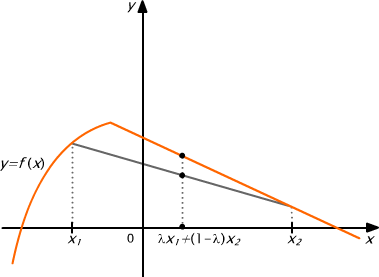
Fig. 6.3

Fig. 6.4

Theorem

Let f  be a function, continuous in an interval P, and differentiable in the interior of P. The function f is

Theorem

Assume a function f is continuous in an interval P and two-fold differentiable in Int P. The function f is

  1. convex in an interval P if, and only if f '' (x) ≥ 0 for every x ∈ Int P;

  2. strictly convex in an interval P if, and only if f '' (x) ≥ 0 for every x ∈ Int P and f ''  is not a null-function on any subinterval of P, of finite length;

  3. concave in an interval P if, and only if f '' (x) ≤ 0 for every x ∈ Int P;

  4. strictly concave in an interval P if, and only if f '' (x) ≤ 0 for every x ∈ Int P and f ''  is not a null-function on any subinterval of P, of finite length.

Corollary

• If f '' (x) > 0 for every x ∈ (a, b), then f is strictly convex in (a, b). If additionally f is continuous in [a, b], then it is also strictly convex in the interval [a, b].

• If f '' (x) < 0 for every x ∈ (a, b), then f is strictly concave in (a, b). If additionally f is continuous in [a, b], then it is also strictly concave in the interval [a, b].

Definition

Let a function f be defined on some neighborhood of a point x0. We say that a point (x0, f (x0)) is an inflection point of the function f, if there exists a number δ > 0 such that on one of the intervals (x0, x0 + δ) or (x0 - δ, x0) the function f is strictly convex, and on the second one it is strictly concave.

Remark

Instead of saying that (x0, f (x0)) is an inflection point of a function f one often says: x0 is an inflection point of f.

Theorem

Assume a function f is continuous in some neighborhood of a point x0.

  1. if x0 is an inflection point of f, then f '' (x0) = 0 or f '' (x0) does not exist.

  2. if f '' (x) changes its sign by passing through the point x0, then x0 is an inflection point of f.

  3. if f ' (x0) = f '' (x0) = ...= f (n-1)(x0) = 0 and f (n)(x0) ≠ 0 and the function f (n) is continuous at x0, then

    (a) if n is odd then x0 is an inflection point of f.

    (b) if n is even then x0 is not an inflection point of f.

Example

We will determine intervals of convexity and inflection points of the function f (x) = e -x².

The domain of f is R. The function f has derivatives of any order in the entire domain. Let us compute the second derivative of f:

Roots and the sign of the second derivative of f are exactly the same as roots and the sign of 2x² - 1, since the exponential function is always positive.

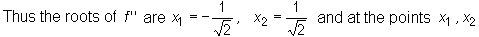the function f '' changes its sign and thus x1 and x2 are the inflection points of the function f. Additionally

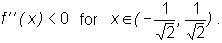
By the above theorems f is strictly convex in the intervals and , and f is strictly concave in .


↔ previous  next ≈