
| ↔ previous | next ≈ |
Theorem
Provided a function f is integrable over an interval [a, b], it is bounded on this interval.
Remark
The inverse theorem is not true, i.e. not every function that is bounded on [a, b] is over this interval integrable.
Example
The Dirichlet function given by the formula

is not differentiable over any interval [a, b], because for a rational ξ k the limit of a sequence of integral sums is the length of the interval [a, b], whereas for an irrational ξ k it equals zero. This means, however, that there is no common limit for an arbitrary choice of arguments of f.
Sufficient conditions for a function to be integrable
Theorem
If a function f is continuous on an interval [a, b], then it is integrable over this interval.
Theorem
If a function f is bounded on an interval [a, b], and has a finite number of discontinuity points, then it is integrable over this interval.
Remark
A finite number of discontinuity points is not a necessary condition for a function to be integrable
Example
The function
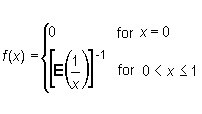
where E denotes the integral part of a number, is integrable over the interval [0, 1], although at points x = 1/n, for n >1, it is not continuous (figure 9.7).

Fig. 9.7
Theorem
If a function f is monotone on an interval [a, b], then it is integrable over this interval.
Theorem (on integrability of a function over a subinterval)
If a function f is integrable over an interval [a, b], then it is integrable over any subinterval of this interval.
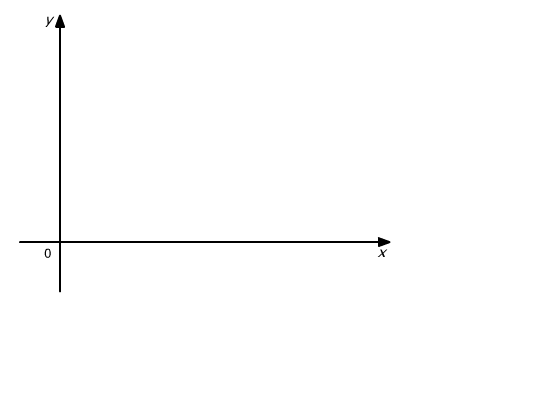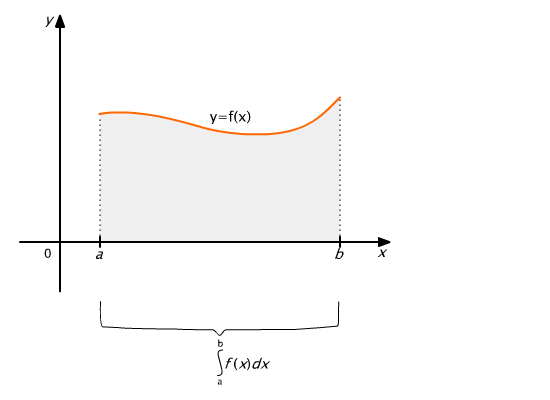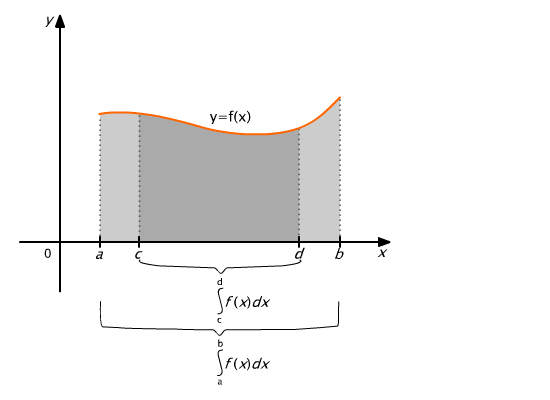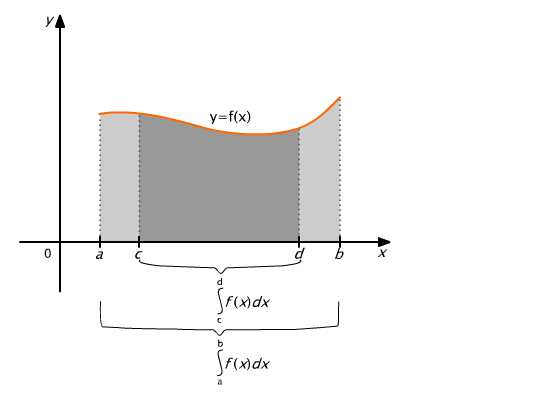
fig. 9.8
Theorem
If a function f is integrable over an interval [a, b], then also a function | f | is integrable over this interval.
Remark
The inverse theorem is not true, which is illustrated by the following example.
Example
The function

is not integrable over the interval [0, 1] (likewise the Dirichlet function), whereas the integral of the function |f(x)| ≡ 1 over this interval equals 1.
If functions f and g take on different values only at finite number of points from an interval [a, b] and one of the functions is integrable on this interval, then the second function is also integrable and both integrals over the interval [a, b] are equal.
Exercise 9.1
using the above theorem calculate the integral
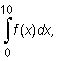
where
![]()
Though the above theorems assure the existence of definite integrals for a lot of functions, they do not provide effective tools for calculations.
Practical methods of calculation of definite integrals are based on theorems we discuss below. Relatively simple proofs of these theorems follow directly from the definition.
Theorem (on linearity of a definite integral)
If functions f and g are integrable over an
interval [a,
b], then the functions f + g and A f ,
where A denotes any constant, are integrable over this interval
too, and
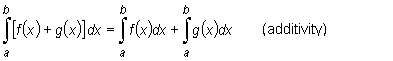 |
"an integral of a sum equals a sum of integrals",
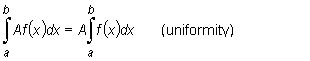 |
"a constant can be moved in front of the integral".
Theorem (on preserving the inequality by integration)
If functions f and g are integrable over an interval [a, b] and satisfy the condition f (x) ≤ g (x), for x ∈ [a, b], then
 |
Theorem (mean value theorem of integral calculus)
If a function f is continuous on an interval [a, b],
then there exists a point ξ
∈
[a, b] such that
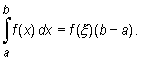 |
For a function taking on nonnegative values, the claim of the above theorem has the following geometrical interpretation: the area under the graph of this function is equal to the area of the rectangle of sides f (ξ) and b - a (figure 9.9).

Fig. 9.9
Definition
An expression
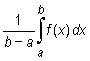 |
is called a mean value (or an integral mean) of a function f over an interval [a, b].
It is a generalization of the well known notion of an arithmetic mean of a finite number of elements.
Theorem (on additivity of an integral with respect to the integration interval)
If a function f is integrable over an interval [a, b], and c ∈ (a, b), then
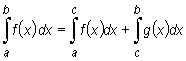 |
Wa take advantage of this theorem by integrating functions defined by different formulae on subintervals of the integration interval.
Example
Integrate the function
![]()
over the interval [-1, 1].
Dividing the integration interval into two subintervals [-1, 0] and
[0, 1] we get

From among all theorems, especially important are the fundamental theorems of the calculus that constitute a connection between notions of definite and indefinite integral.
| ↔ previous | next ≈ |