In many cases finding an antiderivative is very difficult or even impossible. This is especially true for functions that are not elementary integrable or for functions defined only by numerical values. In the latter case, the notion of an antiderivative is even formally meaningless. In such situations one has to use methods of an approximate evaluation of definite integrals.

The main idea of approximate methods (called also numerical methods) is a replacement of an integrand by an easily integrated function. Usually it is a polynomial, which at certain points from an integration interval, called basic points for integration (or abscissas), takes on values identical with the integrand. It can be shown that if x₀, x₁, x₂, ... ,x_n, are basic points for integration, then the formula for an approximate value of a definite integral is of the form

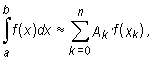whereas the coefficients A_k do not depend on  f.

The above formula is called a quadrature.

The higher degree of the polynomial, the better the approximation. Nevertheless, in practice one uses polynomials of lower degree, mainly because of troubles with an estimation of approximation errors and higher sensitivity to roundoff errors. In order to achieve the required accuracy one has to make use of extended (or composite) quadratures, where the integration interval is divided into subintervals. On each of these subintervals a quadrature of a low degree is used and then the results are summed up.

In the case when the abscissas are spaced apart equally, i.e. the subintervals are of equal width,  of greater practical importance are: the extended trapezoidal rule and the extended. We discuss them in more detail below.

Trapezoidal rule

We divide an integration interval [a, b] into n subintervals (n > 1) of the width

On each subinterval we replace an integrand by a polynomial of the first degree (i.e. by a linear function). The value of the integral on a given subinterval equals the area of a trapezoid, and on the interval [a, b] it is the sum of  n trapezoids (figure 10.12).

Fig. 10.12

Simple transformations lead to the formula

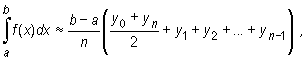where

called  the extended trapezoidal rule.

An estimation of the absolute approximation error (a difference between the exact and approximate value of the integral) for this method is given by the following theorem.

Theorem

If a function f has the continuous second derivative on an interval [a, b], then an approximation error R_n satisfies the inequality

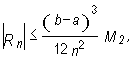where

Required accuracy can by achieved by choosing sufficiently large value of n, but one has to remember that an estimation of the second derivative, necessary for the precise evaluation of the error, may be difficult.

Example

We will make use of the extended trapezoidal rule to compute the approximate value of the integral

.

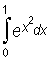Taking n = 5, we estimate the error of this approximation, and next we find for how many abscissas the absolute approximation error is less than  0,01.

Values of the integrand y_k at equally spaced abscissas x_k are listed in the table below.

Substituting we get

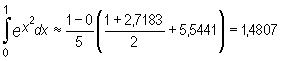
Let us estimate the quadrature error.

We calculate the second derivative of the integrand

On the integration interval [0, 1] it takes on the maximal value f '' (1) = 6e at the point 1. So we can take M₂ = 6e, and the absolute error of the quadrature does not exceed

The requirement that the approximation error should be smaller than  0,01, implies that

that is

Hence n = 12, and the quadrature should have 13 abscissas.

Simpson's rule

In this method  we divide an integration interval [a, b] into 2n subintervals of the width

On each of the subintervals  [a, a + 2h], ... , [a +(2n - 2)h, b], of the width 2h we replace an integrand by a polynomial of the second degree (i.e. by a parabola).  The approximate value of the integral on a given subinterval equals the area of a "parabolic" trapezoid, and on the interval [a, b] it is the sum of  n trapezoids (figure 10.13).

Fig. 10.13

Simple rearrangements yield

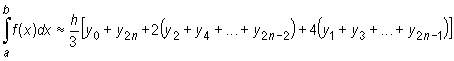where

This formula is called the extended Simpson's rule.

An estimation of the absolute approximation error for this method is given by the following theorem.

Theorem

If a function f has  the continuous fourth derivative on an interval [a, b], then an approximation error R_n satisfies the inequality

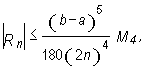where

Quadratures with equidistant abscissas are called  the Newton-Cotes quadratures.

An alternative approach is to make use of quadratures with abscissas that are not necessarily equally spaced.  Such quadratures are called  Gaussian quadratures.

Computer algorithms

A numerical integration is time consuming, especially if high accuracy is required, and therefore this task is done by computers. Appropriate functions are available in math libraries.

Theoretically (as we have seen in the example) the number of abscissas necessary to achieve the required accuracy can be found. However, due to difficulties with estimation of the derivative of an integrand, this task is often practically unfeasible. Hence integration algorithms have usually an iterative character. Approximate values of an integral are computed for an increasing number of subintervals (typically doubled at each step), until either a stabilization in two consecutive steps or allowed number of iterations has been achieved.