1.6 Generalized operations
Union and intersection presented in the
previous sections were two-argument operations. They can be generalized
in a
very simple way for arbitrary finite or infinite number of arguments.
Definition 1.6.1
Let A be a family of sets indexed by a set I , A = {Ai:i
∈ I}. By the generalized union of
the family A we understand the set
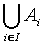
such that x belongs to it if and only if x belongs to at least one
member of the family A. In symbolic notation
x ∈
⎩⎭
i ∈
I Ai iff there is k ∈
I , such that x ∈
Ak .
By generalized intersection of the family A we understand the set
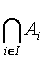
such that x belongs to it if and only if x belongs to all members of
the family A. Shortly,
x ∈
⎧⎫
i ∈
I Ai iff for every k ∈
I , x ∈
Ak .
Obviously, if the set of indexes contains two elements only, for
example I = {1, 2}, then the generalized union is exactly the union of
sets
A1 and A2,

When all sets of the family A are taken from the same universe U,
then the generalized De Morgan's laws hold as it is presented in the
following theorem 1.6.1.
Theorem 1.6.1
For an arbitrary family A of subsets of the universe U, A = {Ai
: i ∈ I} the following equations hold:
- - ⎩⎭ i ∈
I Ai = ⎧⎫ i ∈
I (- Ai )
- - ⎧⎫ i ∈
I Ai = ⎩⎭ i ∈
I (- Ai )
Proof.
Ad. (a) Suppose, x belongs to the left-hand side of the equality
(a). By Definition 1.6.1, x does not belong to any set Ai
for i ∈ I. Thus x is in complement -Ai
for every i ∈ I and, therefore, it
is
in the generalized intersection ⎧⎫ i ∈ I (- Ai ).
Conversely, if x is in ⎧⎫ i ∈ I (- Ai ) then it is in all
sets (- Ai ) for i ∈ I. By
definition of complement, x does not belong to any set of the family A,
and, therefore, it does not belong to the generalized union of the
family
A. Hence x is in - ⎩⎭i ∈ I Ai.
Ad. (b) If x is in - ⎧⎫ i ∈
I Ai , then it is not in the set ⎧⎫ i ∈I Ai.
By Definition 1.6.1 for some particular k, x ∉
Ak. Hence x ∈
-Ak, and therefore x ∈ ⎩⎭ i ∈ I (-
Ai ).
Conversely, if x is in the generalized union ⎩⎭
i ∈ I (- Ai ) then x
must be in at least
one set of the family {- Ai : i ∈
I} and therefore is not in at least one of the set Ai . As
a consequence, x does not belong to the generalized intersection of the
family A and hence x is in its complement.
Example 1.6.1
- Let Ai = {x ∈
R : x < i} for all natural numbers i. Then
⎩⎭ i ∈
I Ai = R and ⎧⎫ i ∈
I Ai = {x ∈ R : x <
0}.
- Let Bi = {x ∈
R : -1/i <x < 1/i} for all natural numbers i>0. Then
⎩⎭ i ∈
I Bi = (-1,1) and ⎧⎫ i ∈ I Bi = {0}.
Question 1.6.1 Let {Ai : i ∈I}
be a family of subsets of a given universe, indexed by a set I .
Which of the following properties are valid?
(1) For every k ∈
I, Ak ⊆ ⎩⎭
i ∈
I Ai.
(2) For every k ∈
I, Ak ⊆ ⎧⎫
i ∈
I Ai.
(3) For every k ∈
I, ⎩⎭
i ∈
I Ai ⊆ Ak.
(4) For every k ∈
I, ⎧⎫
i ∈
I Ai ⊆ Ak.
(5) ⎧⎫
i ∈
I Ai ⊆ ⎩⎭
i ∈
I Ai.
![]()
![]()