If each element of the set X is associated with at most one element of the set Y, then we can say that the function from X to Y was defined. It can be noted shortly as: f : X → Y.

Mapping, transformation and correspondence are the terms that can be used interchangeably with the term function. If some function f associates the element x ∈ X with the element y ∈ Y, it can be noted as f(x) = y, where the element x is called the function's argument, and the element y is the function's value, or the image of the element x.

The set Dom(f) of those elements x to which the function f ascribes values is called the set of arguments or the function's domain. The set Im(f) of those y which are the values of the function is called the set of values or image or function's codomain.

Dom(f) = { x ∈ X : there is an y ∈Y such that f(x) = y}

Im(f) = { y ∈ Y : there is an x ∈ X such that f(x) = y}

Fig. 3.1.1 (a) The example of a function. (b) The graph of a relation which is not a function.

Example 3.1.1

1. Let S be a set of PJIIT students and N be a set of natural numbers. Each student has his own credit book in which the marks for credited lectures are noted. The mapping which associates each student with the number of his credit book is a function that transforms S into the set of natural numbers.
2. The function pictured in the Figure 3.1a associates circles with squares. The association is marked with arrows. The set of this function's arguments is the set of circles, and the set of values, is the set of squares. The Figure 3.1b, however similar, does not picture a function: the first circle is associated with two squares - two values. Such an unclarity cannot happen in the case of functions (but does not prevent the description of a relation!).
3. Let A be an alphabet (i.e. an unempty set), and let A* be a set of words written in this alphabet. We will describe the mapping f, which assigns length to the words (length of the word is the number of symbols of which the given word is composed). For example, if A is made of letters of our alphabet, then f(alphabet) = 8, and f(aaabbb) = 6. Function f is defined in the set A*, and the values are natural numbers.

f : A* → N

Let us consider one more example of a well known function. Let suc denote mapping,

suc : N → N,

which assiociates a natural number with its immediate succesor suc(n) = n+1. Obviously, for each natural number there is a specified subsequent number suc(n): suc(0) = 1, suc(1) = 2, suc(2) = 3 etc. It seems, that similarly we could associate a given number with its predecessor, defining pred: N → N so that

pred(n) = n-1.

However, now the situation has changed slightly. The predecessor of 1 is 0, but what is the predecessor of 0 ? The mapping pred is not defined for the number 0. Such functions are called partial, as opposed to the total function like successor.

What we have said about functions so far leads to a conclusion that each function f : X → Y, determines a set of pairs (x, f(x)) such that no two pairs have the same predecessor. Such a view of the function leads to the following definition:

Example 3.1.2

1. A binary relation defined in product N × N as {(x,y) : x, y ∈ N and y = 2n+1} is a function which assigns to each natural number n the odd natural number 2n+1. Dom(f) = N, Im(f) = NP (the set of all odd natural numbers).
2. The set of pairs (x, x²) for x ∈ R is a binary relation in R. It is a function which associates an arbitrary real number with its square. Dom(f) = R , Im(f) = R+ (compare Fig.2.2.1)
3. Relation r = {(x,y) ∈ R² : x² = y² } is not a function since (1,-1) ∈ r and, simultaneously, (1,1) ∈ r. However, if we limit relation r to the set of natural numbers, assuming r' = {(x,y) ∈ N² : x² = y² }, then such a relation determines a function id : N → N, which values are identical with arguments, id(n) = n for every n ∈ N.
4. Let A be an arbitrary fixed subset of some set X. Function f : X → {0,1}, such that f(x) = 1 when x ∈ A and f(x) = 0 when x ∉ A is called a characteristic function of the set A. The characteristic function of a subset, A = [2,5], of the set of real numbers is shown in Fig. 3.1.2.

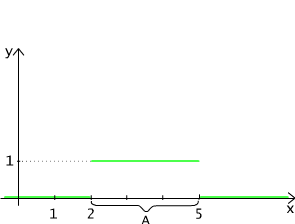
Fig. 3.1.2 The characteristic function of the interval [2,5].

Finite and infinite sequences are special cases of functions. Sequence is a function defined on a set of natural numbers N or its subset N_k (finite or not) of the form [k, k+1, k+2, k+3,..., k+i,...], where k is a fixed natural number and i ∈ N. If the domain of the sequence is an infinite set, then we call the sequence infinite, otherwise the sequence is finite.

If s : N_k → Y, then the value of the function s for the argument k+i is denoted by s_k+i and we call it an i-th element (or the i-th term) of the sequence s. The number k+i its index. The sequence itself is usally presented in the form of a list (s _k, s _k+1, s_k+2, s _k+3,...) or shorter (s_j) _{j ∈ Nk} or, if the sequence is finite, in the form (s_j) _{k ≤ j ≤ n} .

Example 3.1.3

1. Function f : N → N such that f(n) = n! is an infinite sequence with elements (1, 1, 2, 6, 24, 120,...).
2. Function g : N → Z defined by the following formulae g(n) = (-1)ⁿ is an infinite sequnce (1, -1, 1, -1, 1,-1,...) whose set of elements is composed of two values 1 and -1.
3. Function h : N → N whose values determine the number of circles in subsequent triangles pictured in Fig 3.1.3 is a sequence of the form (1, 3, 6, 10, 15,...). Please note, that h(i) = 1+2+...+i = i(i+1)/2 (h is the additive analogs of the factorial). The i-th element of the sequence h is called i-th triangular number.

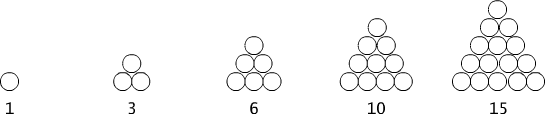
Fig. 3.1.3 Triangular numbers.

Similarly to relations, functions can be visualised as graphs, diagrams or tables. The picture 3.1.4(a) shows the diagram of the function f(x) = |x|,

f(x) = x dla x ≥ 0 and f(x) = -x dla x < 0,

defined in the set of real numbers and of the nonnegative values. Fig 3.1.4(b) pictures the function g mapping the set of real numbers into the set of real numbers, denoted as

g(x) = c wttw c is the samllest integer c ≥ x.

The domain of function g is a set of real numbers, and its codomain is a set of integer numbers. Function g is a so called step (staircase) function. Such a function is denoted with a symbol ⌈ x ⎤.

Fig 3.1.4(c),(d) shows the table of values, and the graph of the function h(x) = (x+2) mod 4 whose values are the remainders of division x+2 by 4.

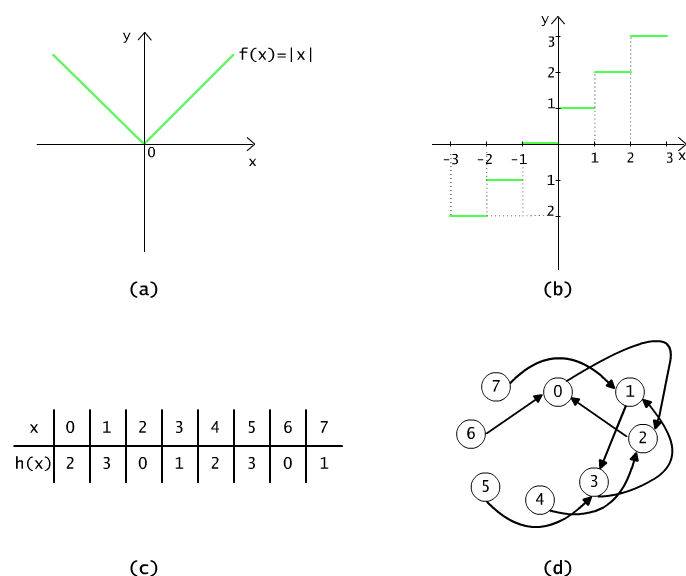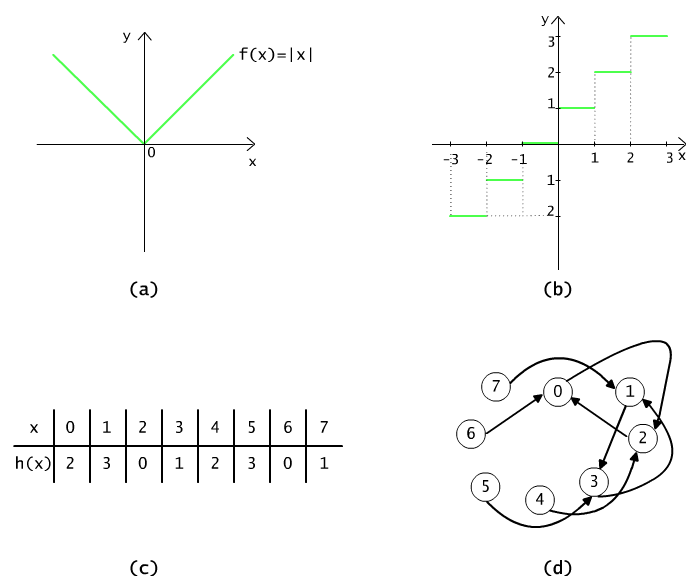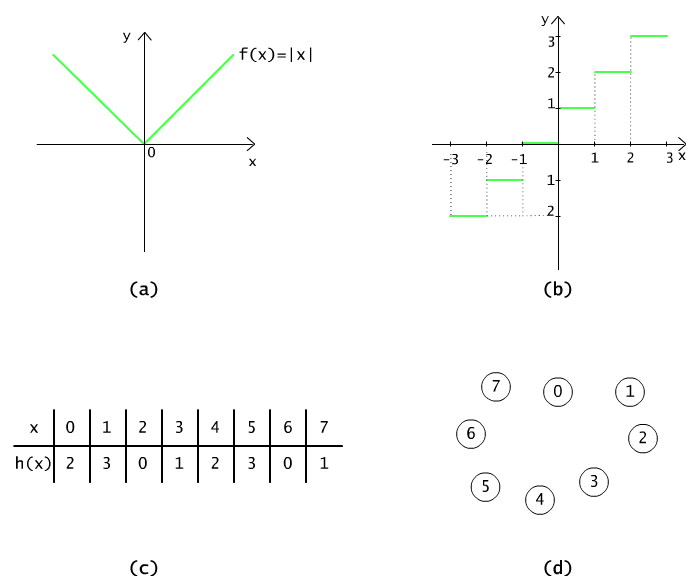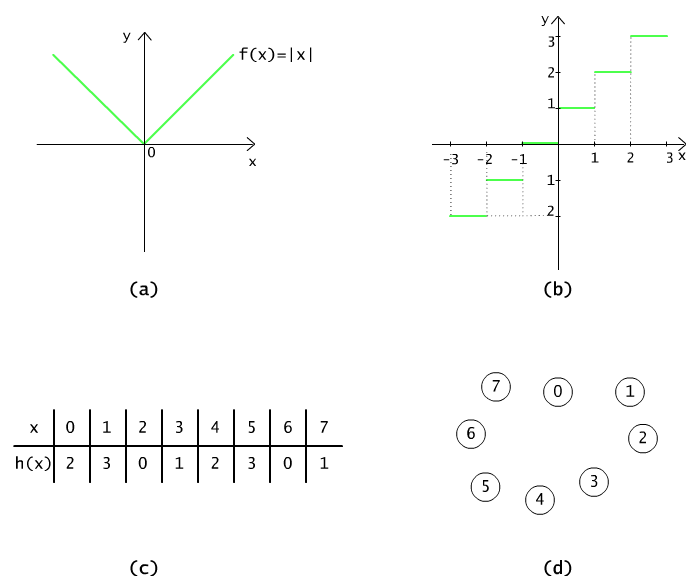
Figure 3.1.4 (a) The diagram of the absolute value function |x|. (b) The diagram of the function entier ⌈ x ⎤. (c) The table of values for the function (x+2) mod 4, and (d) its diagram.

Question 3.1.1: Let f(x) = 2^x be a function defined in the set {0, 1, 2, ...,10}. Determine the codomain of f.

Problem 3.1.1

Draw a diagram of the function f(x) = c where c is the greatest natural number not greater than |x| (the absolute value of x), for x ∈ R.