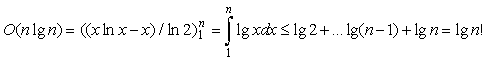
| « previous section |
next section » |
We usually measure the complexity of algorithm by the number of
operations executed. Moreover, we usually take into
account only some characteristic (most costly) operations. This measure
is the most interesting when it is expressed as a function depending on
the size of data. For example, for the Horner's algorithm described in
example 3.5.1(3), the size of data is the order of the
polynomial.
The complexity of this algorithm
can be described by a function T(n) = n, expressing the fact that to
calculate the value of polynomial of order n we have to run
n iterations of the loop. Having such information, we can calculate
the time needed to compute the value of the polynomial of the order 100
on any computer. It is:
(The constant correspond to the cost of the assignment
instructions
at the beginning of the algorithm).
Function, defining the complexity of algorithm, is supposed to determine the cost of the algorithm, but not necessarily expressed in seconds or milliseconds. It is a secondary matter whether the algorithm will perform n or n+3 operations. We do not care either about multiplicative constants. However it is crucial whether the complexity is expressed by the linear function f(n) = n or cubic function f(n) = n3, and how the algorithm will behave for large n. Moreover, we are much more interested in the order of the cost and the intensity of it's increasing to infinity, than in the accurate numbers. The complexity of algorithm will be used as a criterion for or against the use of the given algorithm.
Example 3.6.1
Suppose, we have 6 algorithms of the complexity lg n, n, n2, n3 and 2n respectively. The table in the Fig 3.6.1 gives the estimation of the maximal size of data, which could be crunched (solved) with an algorithm of a given complexity in a given time, on a computer which can execute 106 operations per second. For example, in the time of 1 sec one can solve the problem of the maximum size 1000 with the algorithm of the complexity T(n)= n2 , while in the same time the algorithm T(n)=2n can solve at the most the data of the size 19. It is worth noticing, how slowly the size of the problem changes with the increase of the execution time, when we are dealing with the complexity determined by the exponential function 2n. The values greater than 1010 were mark with the symbol ∞.
|
time\complexity |
lg n |
n |
nlgn |
n2 |
n3 |
2n |
|
1sec |
∞ |
106 |
63*103 |
103 |
100 |
19 |
|
1min |
∞ |
6*107 |
28*105 |
77*102 |
390 |
25 |
|
1h |
∞ |
36*108 |
13*107 |
60*103 |
15*102 |
31 |
Fig. 3.6.1
To classify the growth of functions we use so called asymptotic
notations. In general, we are interested in the order of asymptotic
complexity, i.e. whether it is linear, or quadratic etc. One which we
will use frequently is O-notation (Big O
notation). It is used to describe an asymptotic upper
bound for the magnitude of a function in terms of another, usually
simpler and known, function. The idea is to reduce complicated
functions to
simpler ones whose behavior is better known and easier to understand.
Definition 3.6.1
Let f and g be two functions form the set of natural numbers into R+.
We will say, that f = O(g) iff there are a constant c>0, and a natural number n0 such that for every natural number n > n0, f(n) ≤ c*g(n).
Analogously, we will say that f = Ω (h) iff there are a constant c>0, and a natural number n0 such that for every natural number n > n0, c*h(n) ≤ f(n).
If both above conditions are valid simultaneously f = O(g) and f = Ω (g), then we say that function f has the same order as function g, and we denote it shortly as f = Θ(g).
If f = O(g), then function g estimates from above the values
of
the function f for large enough n. Differently
speaking, function g's rate of increase to infinity is faster than that
of function f. The O-notation means that the function f is bounded from
above
by a function which varies like g.
If f = Ω
(g), then function g estimates the values of function f from below for
large enough n, which means that function g increases to infinity
slower than function f.
Note that equality used in asymptotic notation is purely conventional; one cannot apply usual properties of equality. For example, f = O(g) and h =O(g) do not imply that f = h.
Example 3.6.2
n= 2 * 3/2 * 4/3 * ...* n/(n-1)
In the above equality, we have (n-1) elements, of which each is ≤ 2. That is n ≤ 2n-1 < 2n.
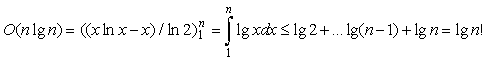
Question 3.6.1 Which of the equalities below are true?
1. n2/100 + 500n = O(n)
2. n3/2 + n2 = Ω (n3)
3. 2n = O(2lgn)
4. n = O(2lgn)
The following theorem allows us to use the methods of the mathematical analysis to compare the rate of functions increase.
Theorem 3.6.1
Let f : N → R+, g : N → R+ and lim n → ∞ f(n)/g(n) = c, where c is a given constant. Then
We omit the proof of the theorem. Instead, let us consider the example of functions f(n) = √ n and g(n) = lg n. Since (lg n)/ √ n with n increasing to infinity is decreasing to 0,
then according to the above theorem function lg increases to infinity faster than function √, that is g = O(f) and , f ≠ Θ (g).
Question 3.6.2
Compare the orders of functions f(n) = lg n (logarithm for the base 2) and g(n) = log n (logarithm for the base 10).
| « previous section |
next section » |