Example 4.1.1

Let X denote the set of automobiles which were produced in the years  1951-2000. We define in the set X the relation  ∼ in such a way, that for every  x, y ∈ X,

x ∼ y iff automobiles  x and  y were produced in the same year.

The relation defines in the set  X fifty groups or classes. Let us denote these classes by the subsequent Roman numbers  I, II, III,...L in such a way that the class  XL contains all automobiles produced in the year 1990, and the class V all automobiles produced in 1955 and only of this year. Suppose that an insurance fee depends on the year of production of an automobile. Now, instead of calculating the fee in an individual way for every  x ∈ X, it suffices to define a function Fee on classes  I, II, ..., L. Fee(IX) = y denotes that the owners of automobiles produced in the year 1959 are to pay amount of y euro.

Let us remark that the relation ∼, defined above, is reflexive  (for every x, x ∼x), is symmetric (for every x, y, if x ∼y, then y ∼ x) and is transitive (if x ∼ y and y ∼z, then all three automobiles x, y, z were produced in the same year, in particular x and z are of the same year). The properties of reflexivity, of symmetry and of transitivity of equality = of numbers passed to the relation  ∼.

It is commonly accepted that the symbol of equivalence  is put in between the arguments, as it is done for  most binary relations.

The following relations are exemplifying the notion of equivalence relation:
- equality relation,
- relation of "being parallel to" among the lines on a plane,
- relation of similarity of triangles.
Another example of the equivalence relation is the following relation ∼ defined in the set  R^R of all functions f : R → R and described as follows: for any pair of functions f, g from the set  R^R ,

f ∼ g iff f(x) = g(x) for every x ∈ R.

For example, the functions (x+1)*(x+1) and x² +2x +1 take the same values for every argument, hence they are in the relation  ∼. This relation is usually denoted by the symbol =, hence we write   (x+1)*(x+1) = x² +2x +1  for all x in R.

Observe that the relation r defined in the set  R^R by the formula

f r g iff f(x) = g(x) for a certain x ∈ R,

is not an equivalence relation. The relation r is reflexive and symmetric, however, it is not transitive. Consider three functions  f(x) = x, g(x) = x², h(x) = 2^x. We have  (f, g) ∈ r , since f(1) = g(1) =1, and  (g, h) ∈ r, since g(2) = h(2)= 4, however, there is no  x ∈ R, for which 2^x = x (observe that always x < 2 ^x ). We are calling the attention of the reader to the subtle difference in the definitions of the relations  ∼ and  r. In the first case the equality of values was required for all arguments of the two functions, in the second case, the relation r holds for the two functions f and g if there exists one point x such that f(x) = g(x). This condition is too weak to guarantee the transitivity of the relation r.

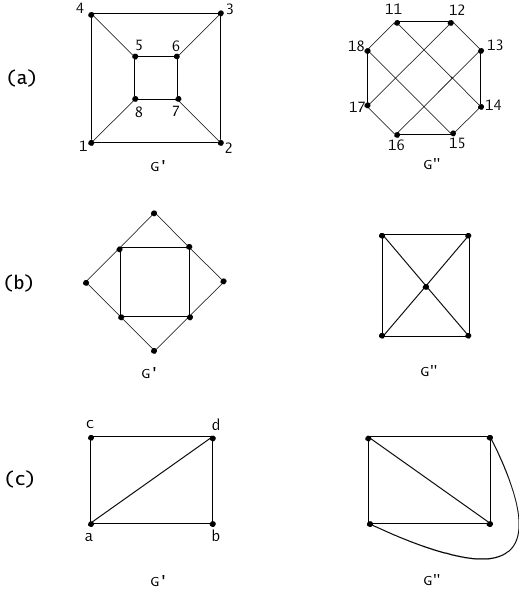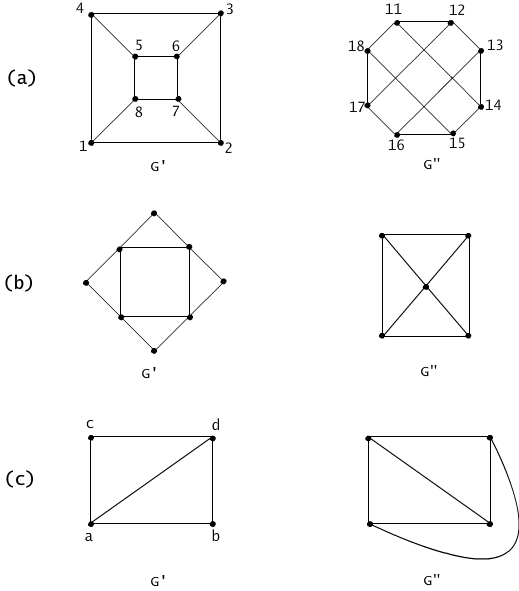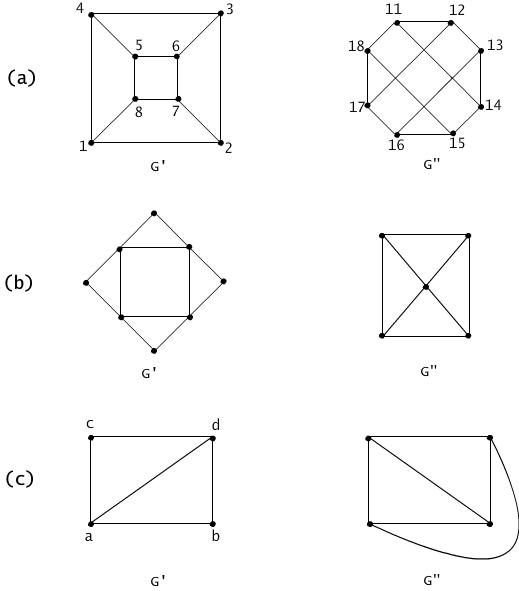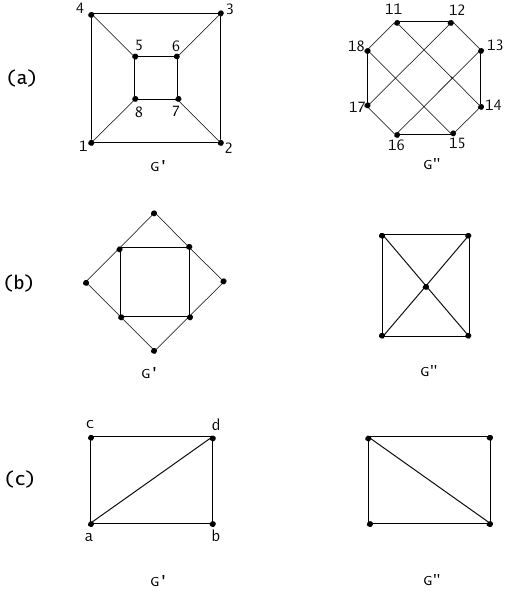
Fig. 4.1.1 (a) Function f(i) = 10+i is an isomorphism mapping graph  G' onto G". (b) An example of non-isomorphic graphs (the sets of nodes have different cardinalities). (c) An example of non-isomorphic graphs (the degree of vertices are different).

Question 4.1.1: Is the relation  r defined for arbitrary subsets A, B of a set X by the condition

A r B iff A ∪ B = B,

an equivalence relation?

Example 4.1.2

(1) Consider the set P of programs written in a programming language (without loss of generality we can assume they are written in Java). We define a binary relation between programs in the following way:

p₁ ≈ p₂ iff for arbitrary data d, the program  p₁ terminates its computation for d iff the program  p₂ terminates its computation for  d, and  if for the same data both programs have finite computations, then the results are identical.

This relation is reflexive, symmetric and transitive. Hence, it is an equivalence relation. Let us observe that two programs equivalent in the just defined sense, may differ essentially, for example, their costs may be different.

(2) Let  G'= <V', E'> and G" = <V", E"> be two graphs, let  f be a bijection from the set of nodes  V' onto V", f : V' → V", and such that  it preserves the relation of adjacency, i.e. for every v', u' ∈ V',

(v', u') ∈ E' iff (f(v'), f(u')) ∈ E".

We say that the function f is an isomorphism mapping graph  G' onto graph G'' and that two graphs are isomorphic.

Let us consider now the relation  ≈ which relates two graphs G' and G" if and only if there exists an isomorphism from  G' onto  G". 

The graphs illustrated on Figure  4.1.1(a) are isomorphic. The function f(i)= 10*i defines a one-to-one correspondence from the first graph onto the second which preserves the adjacency relation. The graphs illustrated on the Figure  4.1.1(b) are not isomorphic since they differ in the number of nodes. Graphs illustrated on the Figure 4.1.1(c) are not isomorphic since one of the graphs has all nodes of degree 3 and the second graph has only two nodes of degree 3.

The relation  ≈ considered in an arbitrary set of graphs is the equivalence relation. Indeed,

• it is reflexive, since each graph is isomorphic to itself (the isomorphism is established by the identity function f(x) = x),

• it is symmetric, since if a function f establishes an isomorphism between  G' and G" , then f ^-1 defines an isomorphism between G" and G',

• it is transitive, since if f is an ismorphism from  G to G', and  g an isomorphism from  G' to G", then their composition f ° g is an isomorphism from G to G".

Problem 4.1.1

Prove that the relation of similarity of triangles ∼ which holds between two triangles on a plane if and only if they have all the angles equal, is an equivalence relation.

Solution. Evidently, this relation is reflexive: each triangle is similar to itself. The relation is, in an obvious way, symmetric. In order to prove the transitivity we assume that  Δ₁ ∼ Δ₂ and Δ₂ ∼ Δ₃. Now, if angles of the triangle  Δ₁ are α, β and γdegrees, then triangle Δ₂ has angles α ,  β, and  γ. Similarly, the angles of triangle  Δ₃, as equal to the angles of  Δ₂, are also α, β and γ. Hence Δ₁ ∼ Δ ₃. 

Proof.

Reflexivity: If f is a function onto, then for every x there is exacly one value  f(x) and obviously f(x) = f(x).

Symmetry: The relation of equality = is a symmetrical relation, and since the values  f(x) and f(x') are defined, hence f(x) = f(x') implies f(x') = f(x). As a consequence  x ≈ x' iff  x' ≈ x.

Transitivity: If  x ≈ x' and x' ≈ x'', then the values of function f for x, x' i x'' are equal, hence x ≈ x''. ♦

Lemma 4.1.1 provides a simple method of constructing an equivalence relation.  However, if the function f is an injection (one-to-one function) then the relation defined in this way is the identity relation.

Example 4.1.3

n ≈ m  iff  f(n) = f(m)

such that any natural number divisible by 3 is in the relation with number  0 (since they give the remainder 0), all natural numbers which  divided by 3 give the remainder 1 are in relation ≈ with number 1, and finally, all natural number which divided by 3 give the remainder 2 are in relation with number 2. The realtion  ≈ defines a partition of the set N of natural numbers onto three sets.

(2) Let  G = <V, E> be an undirected graph where V is the set of nodes and E is the set of edges of the graph. We define a relation ∼ in the set V of nodes,

x ∼ y iff there exist a path in G from node x to node  y.

The relation defined in this way is an equivalence relation in the set V of nodes of the graph G. We say that it is a transitive closure of the adjacency relation of nodes.  Reflexivity and symmetry of the relation  ∼ are evident. Let us check the transitivity property. If  x ∼ y and y ∼ z, i.e. if there exists a path from node x to node y and a path from node y to node z then obviously their juxtaposition is a path from node x to node z, c.f. Figure 4.1.2(a). In the graph of Figure 4.1.2(b),  we see that the relation ~ determines a partition of the set V of nodes onto two groups (they are called connected components of the graph). Figure 4.1.2(b) illustrates the reachability graph. There is no path connecting a node from one group to another node in the other group. In each group, however, every node is reachable from any other. If a graph has such property it is called a connected graph. The graphs of Figure 4.1.1 are connected, and the reachability graph is a complete graph i.e. every node is connected by a node with any other node.

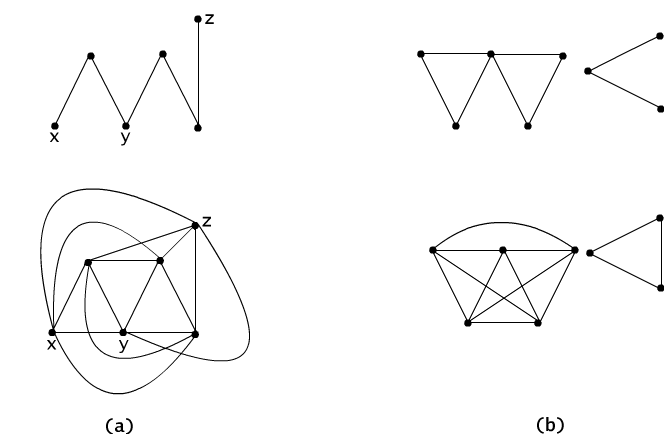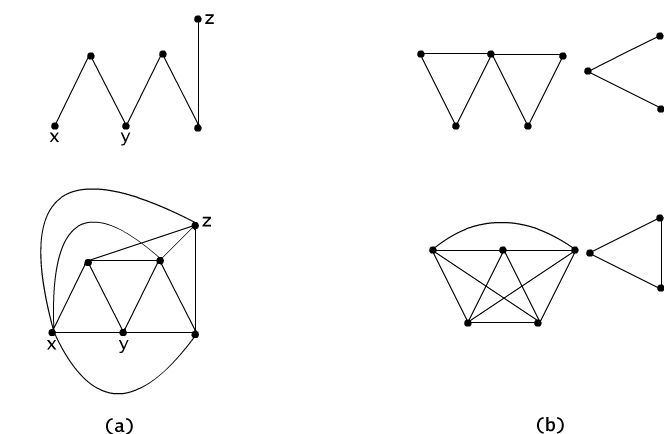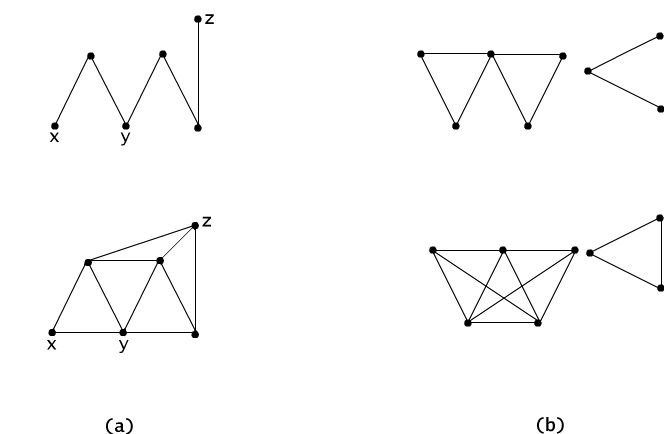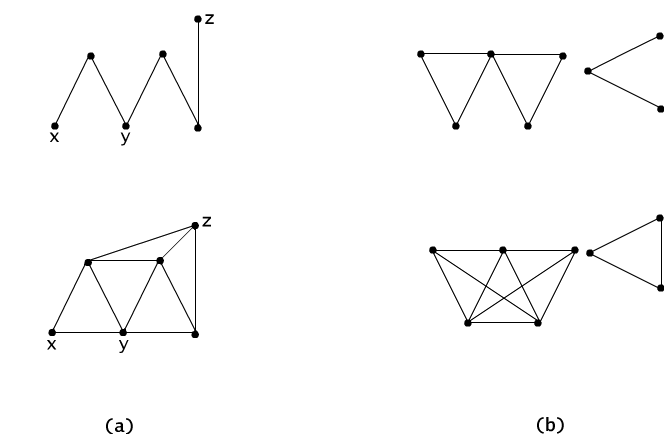
Fig. 4.1.2 Graph and its transitive closure:  (a) in the case of connected graph, (b) in the case of disconnected graph.

An equivalence relation, as any binary relation, may be presented in a graphic form. The reader will observe the specific shape of the graph:

the set of nodes of a graph is divided onto separated, disjoint groups. Figure  4.1.3 illustrates in a graphical form two equivalence relations defined by two formulas y = x mod 3 and y= x mod 4 in the set {0,1,2,3,4,5,6}.

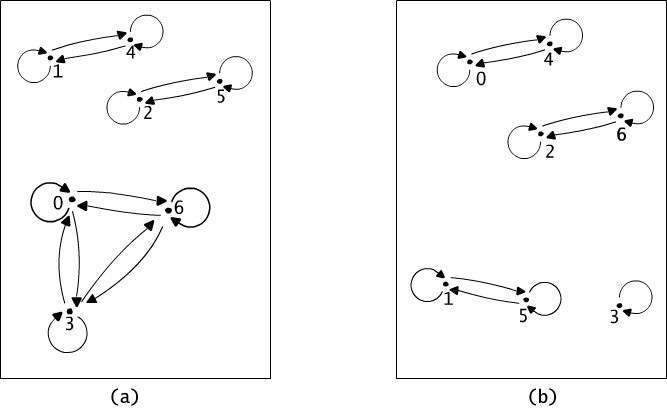
Fig. 4.1.3 Two equivalence relations on the set {0, 1, ..., 6} determined by: (a) formula y = x mod 3, (b) formula y = x mod 4.

Question 4.1.2 Is the union of two equivalence relations an equivalence relation?

Question 4.1.3 Check, whether the relation  r defined on the set R of real numbers by the condition: for every x, y ∈ R,(x, y) ∈ r iff x-y ∈ Q, is an equivalence relation.

« previous section

next section »