Consider the set of students of a University. In a natural way we can distinguish two groups: women and men. Thus we have divided the set of students onto two disjoint classes. Assuming that among our students there are women and men, the classes are non-empty. In a similar way one can partition the set of all students onto the groups with respect to their progress. So we have a group of students of the first year, a group of students of the second year, ..., a group of students of the fifth year. All of them are non-empty sets.
The mathematical formalization of the notion of partition is given below.  

Let us consider the following partition of a plane determined by the axes of the system of coordinates:

Each point belongs to exactly one subset, c.f. Figure 4.3.1(a)

Another partition of the same plane is given by the sets {(x, y) ∈ R² : x ≥ 0}, {(x, y) ∈ R² : x<0 } shown on Figure 4.3.1(b). In this partition each point belongs to either left or right halfplane.

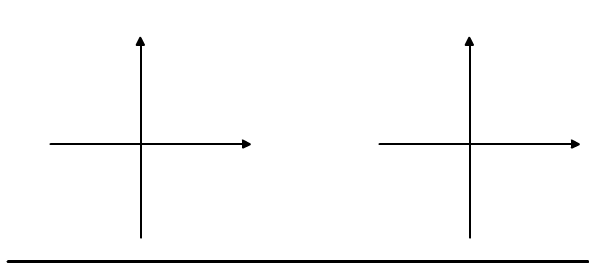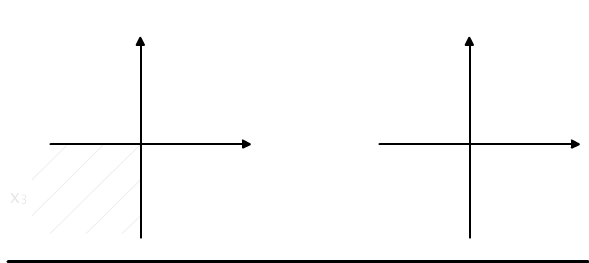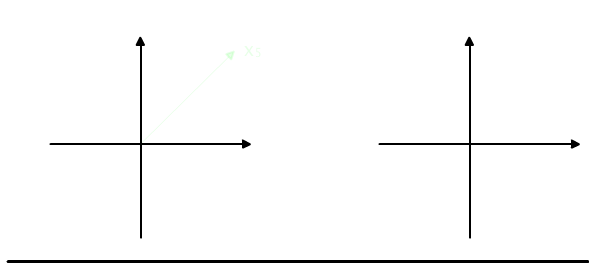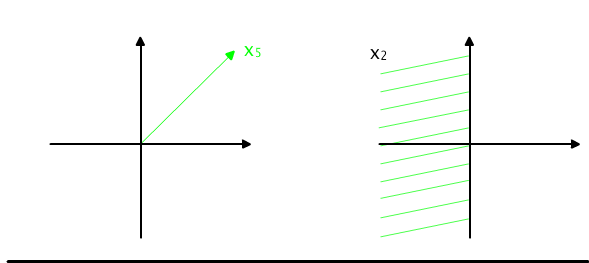
 Fig. 4.3.1 (a) Partition of the plane onto 5 parts. (b) Partition of the plane onto 2 parts.

Example 4.3.1

Let  K(x) be a set of points of a circle with the center in the origin O of the system of coordinatesand of radius x, x ∈ R ^≥0. Let us assume additionally that the origin O is the circle of radius 0. The family of all circles K(x) for  x ∈ R ^≥0 is a partition of plane. Indeed, every circle is a non-empty set. Every point belongs to a certain circle (the point of coordinates (x, y) belongs to the circle  K( √ (x² +y²)). Moreover, for every two different real numbers x and x',  circles K(x) and K(x') are disjoint.

Question 4.3.1  Let X₁ = {x ∈ N: x is the square of an even number}, X₂ = {x ∈ N: x is a prime number}, X₃ = {x ∈ N: x is the square of an odd number}. Does this family form a partition of the set of all natural numbers N?

« previous section

next section »