| « previous section | next section » |
A given ordering relation ≤
in
a set X allows to define an ordering relation in the set of
n-tuples
of elements of X. Let x1, x2, ...xn,
y1, y2, ...yn ∈
X, we put
(x1, x2,...xn ) ≤ (y1, y2,...yn) iff for all i ≤ n , xi ≤ yi.
Indeed, the relation defined above is a partial order in the set Xn. This partial ordering is called a product order.
Question 5.6.1 Let S be the english alphabet. Which of the two tuples is earlier in the product order in S5: (P,O,L,I,S,H) or (P,O,L,A,N,D)?
Let X be the set N of natural numbers with the ordering relation ≤ and let n=3. The produt order ≤ in N3 compares the triples of natural numbers. The Figure 5.5 presents a fragment of the Hasse diagram of this relation.
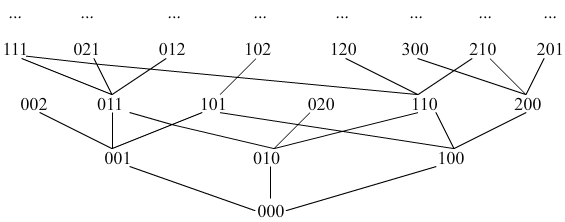
Fig. 5.6.1 A fragment of the Hasse diagram of product ordrer in the set N × N × N.
It is obvious that such an ordering relation is not total: although the triplets (5, 4, 3) and (2, 3, 8) differ neither of the two possibilities holds (5, 4, 3) ≤ (2, 3, 8) and (2, 3, 8) ≤ (5, 4, 3).
Is it possible, starting from a given linear ordering in the set X, to define a linear order in the set Xn ?
Let us come back to the natural numbers. When n = 2, it is easy to establish a total order using pair-function f(n, m) = n + (n+m)*(m+n+1)/2 (see example 3.2.1(3)) and usual ordering ≤ in N as follows:
(n, m) ≤ (x, y) iff f(n, m) ≤ f(x, y).
The binary relation defined in this way, is reflexive, transitive,
which is the immediate consequece of properties of the relation ≤ in the set of natural numbers. The
relation ≤ is antisymmetic
since f is a one-to-one function. Indeed, if (n, m) ≤ (x, y) and (x, y) ≤
(n, m), then f(n, m) ≤ f(x, y) and f(x, y) ≤ f(n, m). Thus f(n, m) = f(x, y), and therefore
(x, y) = (n, m). Since, no matter what two pairs of
natural numbers are chosen, they can be compared by the relation ≤. Hence, the relation is a total ordering.
Another way to define a total order in the set of ordered pairs of
natural numbers is to put a pair (n, m) before the pair (n', m')
whenever n < n', or when n = n' and m < m'. Hence, the pair
(5,7) is before (6,7) and before (5,8). The idea of this ordering can
be generalized as in the Definition 5.6.1.
Definition 5.6.1
Let < Xi , ≤ i > for i =1,...,n, be ordered sets. We define a binary relation ≤* in the product X1 × X2 × X3 ... × Xn by
(x1, x2, ...xn ) ≤* (y1, y2, ...yn) iff either for every i ≤ n , xi = yi
or there is k, 0< k ≤ n, such that for 0< i < k , xi = yi and xk ≤ k yk, xk ≠ yk.
The binary relation defined in this way is called a filing order in X1 × X2 × ... × Xn.
In other words, the n-tuple (x1, x2, ...xn
) is before the n-tuple ≤* (y1,
y2,
...yn) in the ordering ≤*
, if the first xi, which is different from yi,
comes before yi in the set Xi.
Lemma 5.6.1
If < Xi, ≤
i > is a partially orderd set for i ∈
I, then the filing order ≤* is
a partial ordering in the product X1
× X2 ×
... × Xn.
If all sets
< Xi, ≤
i > for i ∈
I, are linearly ordered, then ≤*
is a linear order too.
Example 5.6.1
Consider the sets X1 = X3 = {1, 2,... 9}, X2 = {a, b, ...z} with the usual ordering relation in the sets of numbers and with alphabetic order in the set X2. The relation ≤* is a linearly order in the set of triplets of the form (digit, letter, digit), in such a way that (1,a,1) ≤* (3,b,2) ≤* (3,c,1) ≤* (5,a,2) etc.
Note that dictionaries are usually constructed similarly. When we consider words of the same length then the order of words is determined by the alphabetic order in a way described in the definition 5.6.1.
kajak ≤* kojec ≤* kolec ≤* pokaz.
In general, words in a dictionary have different lengths. To compare
them we usually use some extention of the filing order ≤* , denoted by ≤
L and called the lexicographic order.
Definition 5.6.2
Let Σ be a fixed alphabet linearly orderd with a relation ≤. By the lexicographic order we understand a binary relation ≤ L Σ* defined in Σ* as follows (x1, x2,...xn ) ≤ L (y1, y2,...ym) iff
either n ≤ m
and for all 0< i ≤ n , xi =
yi or
there is k, 0< k ≤ min(n,m), such that xk
≤k yk, xk
≠ yk and xi =
yi for all i, 0< i < k.
Lemma 5.6.2
The lexicographic order ≤L is a total order in Σ*.
Question 5.6.2 What is earlier in the lexicograpic order ≤ L "egg " or "hen" ?
| « previous section | next section » |