We notice all values which satisfy the propositional function   α(x) by {x∈X: α(x)}. More strictly, we should write

but we usually use a shorter form providing that it does not lead to misunderstanding.

Every propositional function determines some subset (some property) of the space in which it is defined, namely the set of this arguments for which the propositional function is satisfied.

Proof.

We prove only the first of the mentioned formulas (The Reader can prove the remaining two using a similar method).

Let a ∈ {x ∈X: α(x)} ∪ {x ∈X: β(x)}. Then, according to the definition of the union of sets, the element a belongs to at least one of the sets {x ∈X: α(x)}, {x ∈X: β(x)}. It means that a satisfies the propositional function α(x) or satisfies the propositional function β(x), that is the disjunction α(a/x) ∨(a/x) is true. Hence a ∈ {x ∈X: α(x) ∨ β(x)}.

Conversely, if a ∈ {x ∈X: α(x)∨β(x)}, then α(a/x) ∨β(a/x) is a true proposition. Using two-argument Boolean algebra (see subsection 6.2) at least one of propositions α(a/x), β(a/x) is true. It follows that a belongs to the set {x ∈X: α(x)} or to the set {x ∈X:β(x)} (or both), i.e a ∈ {x ∈X: α(x)} ∪ {x ∈X: β(x)}. ♦

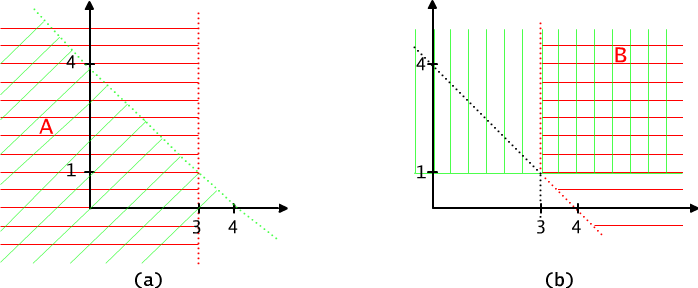
Fig. 7.2.1 Set of plane points that satisfy (a) the propositional function ((x-3 < 0) ∨(x+y< 4)), (b) the propositional function ¬ ((x-3 < 0) ∨ (x+y< 4)) ∧ (y ≥ 1).

Example 7.2.1

1. Let ¬ ((x-3 < 0) ∨(x+y < 4)) ∧ (y ≥ 1) be a two-argument propositional function over the set of real numbers.To fix the set of arguments which satisfy this function, first we find the set of all pairs (x,y) which satisfies the propositional function ((x-3 < 0) ∨ (x+y < 4)). Let A = {(x,y) ∈ R²: ((x-3 < 0) ∨(x+y < 4))} = {(x,y) ∈ R²: x<3}∪ {(x,y) ∈ R²: x+y<4}, see Fig. 7.2.1(a). Then by making proper operations on sets (i.e. estimating -A ∩ {(x,y) ∈ R²: y ≥ 1}) we find all pairs which satisfy our propositional function. The result is the set of all pairs  (x,y), for which x ≥ 3 and y ≥ 1, as presented on Fig. 7.2.1(b).
2. The three-argument propositional function (A ∪ B ⊆ C → (A ⊆ C ∧ B ⊆ C)) over subsets of some space U is satisfied for all elements of the product P(U)³. Indeed, if we put any arbitrary sets in the place of the variables A, B, C, the obtained proposition is true. Actually, the condition A ∪ B ⊆ C is equivalent to (A ∪B) ∪ C = C, thus A ∪ C = A ∪ (A ∪B ∪ C) = A ∪ B ∪ C = C and B ∪ C = B ∪ (A ∪ B ∪ C) = A ∪ B ∪ C = C and therefore  A ⊆ C and B ⊆ C, see subsection 1.3. 

Question 7.2.1 Find the values of x which satisfy the propositional function ((x ≤ 1 ∨ x >1) → x² =1) in the set of all real numbers.

« previous section

next section »