We wstępie do swojej książki "Grafy i hipergrafy, Berge napisał, że teoria grafów jest dziedziną zadziwiającą. Pojawiła się jako osobliwość, zabawka w matematyce, potem stała się dla Gustawa Kirchhoffa narzędziem badania obwodów elektrycznych,a potem była stosowana w chemii, psychologii i ekonomii. A wszystko to zanim sama na dobre powstała, zanim utrwaliła swoje pojęcia podstawowe i fakty. Zanim zostały zbudowane jej matematyczne podstawy. Teoria grafów jest dziedziną, która pokazuje jak praktyka wpływa na teorię i odwrotnie. Przedstawienie najważniejszych pojęć teorii grafów poprzedzimy krótką historyjką związaną z narodzinami tej teorii. Otóż szwajcarski matematyk Leonard Euler, przebywając w Królewcu na zaproszenie Carowej Katarzyny, miał zwyczaj spacerować po mieście. Poszczególne części miasta, położonego na obu brzegach rzeki Pregoły i jej dwu wyspach, połączone były siedmioma mostami, por. Rys.3.0(a). Euler starał się znaleźć taką drogę, która pozwoliłaby mu przejść dokładnie raz po każdym z mostów i wrócić do miejsca wyjścia. Rozwiązanie problemu mostów królewieckich ukazało się w pracy Eulera opublikowanej w 1736 roku, dając początek nowej teorii - teorii grafów.

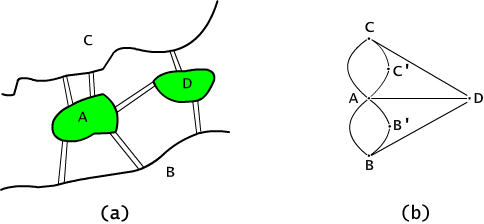
Rys. 3.0 (a) Szkic planu Królewca i (b) odpowiadający mu graf.

Obecnie grafy okazały się niezastąpionym narzędziem do modelowania systemów rzeczywistych. Dzięki temu, że posiadają prostą reprezentację graficzną, łatwo przemawiają do wobraźni, ułatwiają zrozumienie pojęć i faktów.
W tym wykładzie omówimy podstawowe definicje dotyczące grafów zorientowanych i niezorientownych. Omówimy pojęcie drzewa i jego elementarne właściwości.