| « poprzedni punkt | następny punkt » |
Grafy, o których będzie mowa w tym wykładzie, to proste figury geometryczne składające się z punktów i odcinków lub strzałek łączących niektóre z nich. Tak właśnie ilustrowaliśmy relacje. Matematyczna definicja grafu odsyła nas do pojęcia relacji.
Definicja 3.1.1
Grafem zorientowanym (digrafem albo grafem skierowanym) nazywamy parę uporządkowaną G = <V, E>, gdzie V jest niepustym zbiorem, a E podzbiorem produktu V × V. Elementy zbioru V nazywamy węzłami lub wierzchołkami grafu, a elementy zbioru E nazywamy krawędziami grafu.
Każdy graf jednoznacznie wyznacza pewną relację binarną w zbiorze V,
(x, y) ∈ r wttw (x, y) ∈ E.
Odwrotnie, każda relacja binarna r w zbiorze X, wyznacza
jednoznacznie
graf zorientowany, którego węzłami są elementy zbioru X, a krawędziami
uporządkowane
pary
(x, x') należące do r. Relację r będziemy nazywać relacją sąsiedztwa.
Wierzchołki połączone
krawędzią będziemy nazywać sąsiednimi. O krawędzi (x,x') mówimy, że
jest incydentna z wierzchołkami x i x'. Wierzchołek x nazywamy
początkiem, a x' końcem krawędzi (x,x'). Krawędź, której początek jest
identyczny z końcem nazywa się pętlą w grafie.
Powiemy, że graf zorientowany jest skończony, jeśli zbiór jego
wierzchołków jest skończony.
Przykład 3.1.1
Kilka przykładów
grafów
zostało już przedstawionych jako ilustracje relacji binarnych. Typowymi
przykładami grafów zorientowanych są schematy różnego rodzaju sieci:
np.
sieć
dróg, sieć wodociągowa, sieć telekomunikacyjna, itd. Na
rysunku 3.1.1(a) przedstawiamy graf
połączeń
drogowych między pewnymi miastami w Polsce.
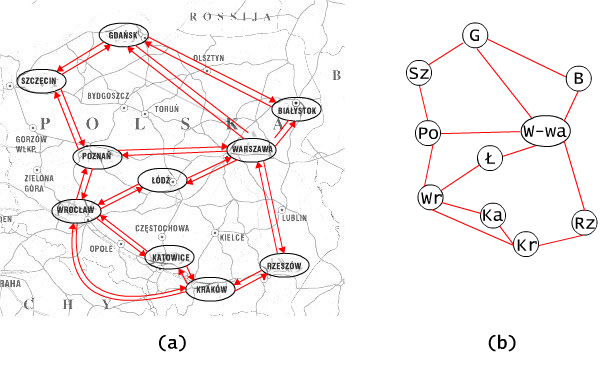
Rys. 3.1.1 Graf przedstawiający sieć połączeń drogowych.
Przykład 3.1.2
Przyjmijmy, że jako szef firmy budowlanej otrzymałeś, drogi Czytelniku, zlecenie zbudowania domu. Jak zabierzesz się do tej pracy? Na początek ustalisz prawdopodobnie jakie czynności trzeba wykonać. Oczywiście, niektóre z nich mogą być wykonywane równocześnie, np. przez różnych fachowców, ale inne muszą być wykonywane w ustalonej kolejności, np. najpierw musimy zbudować fundamenty, a dopiero potem ściany, por. Rys. 3.1.2. Na ogół tych czynności jest bardzo dużo. Jak sobie z tym wszystkim poradzić? Proste, trzeba narysować graf. Wierzchołki tego grafu odpowiadać będą akcjom, które trzeba wykonać w całym przedsięwzięciu, a krawędzie ustalą kolejność w jakiej je trzeba wykonywać. Rysunek tego grafu pozwoli nie tylko objąć całość przedsięwzięcia jednym spojrzeniem, ale i odpowiednio zaplanować terminy rozpoczęcia i zakończenia poszczególnych prac, lepiej wykorzystać czas i wykonawców.
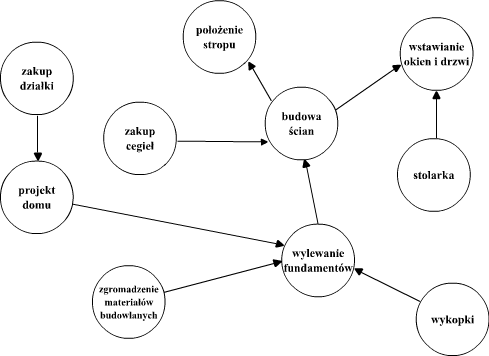
Rys. 3.1.2 Przykład grafu zorientowanego - graf prac budowlanych.
Definicja 3.1.2
Dla każdego wierzchołka grafu zorientowanego definiujemy stopień
wejściowy d+(v) i stopień wyjściowy d-(v)
wierzchołka v
następująco:
Przykład
Stopień wejściowy wierzchołka W-wa na rysunku 3.1.1 wynosi
5, a stopień wyjściowy wierzchołka RZ wynosi 2: d+(W-wa)= 5,
d-(RZ) = 2. Stopień wejściowy wierzchołka "wkonanie
fundamentów" wynosi 3, a stopień wyjściowy 1.
Lemat 3.1.1
Niech G = <V,E> będzie grafem zorientowanym skończonym.
Wtedy S v
∈V d+(v) = S v ∈V
d-(v).
Dowód. Każda krawędź grafu zorientowanego ma swój początek i swój
koniec w pewnym wierzchołku grafu. Końce wszystkich krawędzi zostały
zsumowane po lewej stronie równości, a początki wszystkich krawędzi -
po prawej. Każda z sum występujących w lemacie 3.1.1 jest więc równa
liczbie krawędzi grafu G, cbdo.
Definicja 3.1.3
Powiemy, że graf G = <V, E> jest niezorientowany, jeżeli relacja sąsiedztwa tego grafu jest symetryczna, tzn. dla dowolnych dwóch wierzchołków v, v' ∈ V, (v,v') ∈ E wttw (v',v) ∈ E.
Zatem grafy niezorientowane odpowiadają relacjom
symetrycznym.
W grafie niezorientowanym, jeżeli istnieje krawędź (strzałka) o
początku w v i końcu w v', to jest
też
krawędź o początku w v' i końcu w v. Przykład takiego grafu jest
przedstawiony
na rysunku 3.1.1(a). Zwykle, jeśli mówimy o grafie niezorientowanym,
upraszczamy
rysunek, zastępując strzałki odcinkami, por. Rys. 3.1.1(b). Na
krawędzie
możemy wtedy patrzeć jak na dwuelementowe zbiory, a nie pary
uporządkowane.
Stopniem wierzchołka w
grafie niezorientowanym nazywamy liczbę
krawędzi incydentnych z tym wierzchołkiem. Stopień wierzchołka v
oznaczamy przez d(v).
Lemat 3.1.2
Niech G = <V,E> będzie grafem niezorientowanym, skończonym.
Wtedy suma stopni wszystkich wierzchołków jest równa podwojonej liczbie
krawędzi grafu.
Pytanie 3.1.1 Czy można narysować graf niezorientowany o 2 wierzchołkach stopnia 2 i 3 wierzchołkach stopnia 3?
| « poprzedni punkt | następny punkt » |