| « poprzedni punkt | następny punkt » |
W tym punkcie omówimy pojęcia drogi i cyklu w grafie. Nie będziemy
osobno wprowadzać tych pojęć dla grafów skierowanych i dla
nieskierowanych, ponieważ definicje są takie same.
Definicja 3.2.1
Niech G = <V, E> będzie grafem. Drogą w grafie G nazywamy ciąg wierzchołków v0, v1, ..., vn, taki, że kolejne wierzchołki ciągu są połączone krawędzią, tzn. (vi, vi+1 ) ∈ E dla każdego i = 0, 1, ..., n-1. Długość drogi, to liczba krawędzi, przez które droga przechodzi. Jeśli w tym ciągu v0 = vn, to powiemy, że droga jest zamknięta. Jeśli wszystkie wierzchołki drogi zamkniętej są różne z wyjątkiem pierwszego i ostatniego wierzchołka, to taką drogę nazywamy cyklem.
Jeśli istnieje droga v0, v1, ..., vn,
o początku w v0 i końcu w wierzchołku vn, to
mówimy droga prowadzi od v0 do vn. Ponieważ
rozważamy tylko grafy proste (a nie multigrafy) ciąg wierzchołków
jdnoznacznie wyznacza zbiór krawędzi, przez które droga przechodzi.
Drogę w grafie można więc też zdefiniować jako ciąg krawędzi (v0,
v1), (v1,v2 ), ..., (vn-1,vn),
taki że koniec każdej krawędzi, z wyjątkiem ostatniej, jest początkiem
krawędzi następnej.
Przykład 3.2.1
Przykład 3.2.2
Rozważmy następujący algorytm:
{max := a[0]; i := 1; while i ≤ n do if max<a[i] then max := a[i] fi ; i := i+1 od},
w którym na początku mamy dwie instrukcje przypisania elementu a[0] zmiennej max i jedynki zmiennej i, a następnie instrukcję pętli. Diagram przepływu dla tego programu jest grafem przedstawionym na rysunku Rys. 3.2.1. Wyróżniono na nim dwa wierzchołki: początek, gdy jeszcze nie wykonaliśmy żadnej instrukcji programu i koniec, gdy wszystkie instrukcje programu zostały wykonane. Każdy inny wierzchołek diagramu zawiera instrukcję przypisania lub test jaki trzeba wykonać, jeśli doszliśmy do tego właśnie miejsca w algorytmie. Niektóre strzałki (krawędzie) w grafie mają przypisane słowa tak lub nie by zaznaczyć, którą z krawędzi trzeba wybrać wtedy, gdy mamy do wyboru dwie drogi, zależne od wyniku testu. Czytelnik przyzna, że taki sposób opisu algorytmu jest bardzo intuicyjny. Mając dany ciąg wartości a[0], a[1], ..., a[n] dla jakiegoś ustalonego n, możemy prześledzić na tym grafie każde możliwe wykonanie algorytmu.Każde wykonanie tego algorytmu wyznacza w grafie drogę prowadzącą od wierzchołka "początek" do wierzchołka "koniec". Istnieją jednak takie drogi w tym grafie, które nie odpowiadają żadnemu wykonaniu algorytmu dla żadnych danych. Jakie to drogi? Nota bene: A co robi ten algorytm?
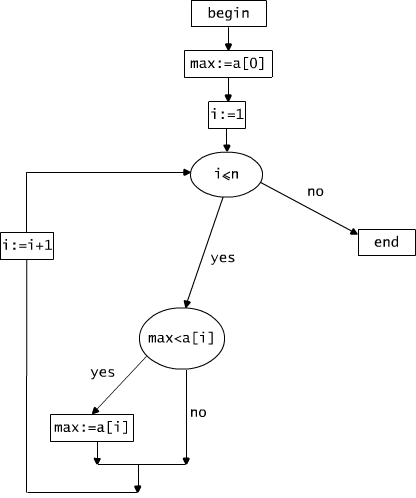
Rys. 3.2.1 Diagram przepływu dla programu przedstawionego w przykładzie 3.2.2.
Pytanie 3.2.1 Podaj przykładowe dane, dla których wykonanie algorytmu odpowiada przejściu po drodze 1, 2, 3, 4, 5, 7, 4, 5, 7, 4, 8.
Drogę nazwiemy prostą,
jeżeli wierzchołki, przez które przechodzi są parami
różne. W konsekwencji, droga prosta nigdy nie przechodzi
dwukrotnie po tej samej krawędzi. Jeśli droga nie zawiera cyklu, to nazywamy ją acykliczną.
Pytanie 3.2.2 Czy droga, której wszystkie krawędzie są różne musi być prosta?
Lemat 3.2.1
Jeżeli w grafie G istnieje droga łącząca dwa różne wierzchołki
u i v, to istnieje też droga prosta i acykliczna prowadząca od u do v.
Dowód. Niech v0, v1, ..., vn, będzie drogą prowadzącą od u do v. Jeśli ta droga nie jest prosta, to istnieją takie indeksy i, j, że vi = vj. Pomińmy wszystkie wierzchołki od pozycji i do pozycji j. Droga v0, v1, ...,vi , vj+1,..., vn, znów prowadzi od u do v. Powtarzając to postępowanie dostateczną liczbę razy, znajdziemy drogę, której wszystkie wierzchołki są różne, otrzymamy więc drogę prostą i bez cyklu.
Definicja 3.2.2
Niech G = <V, E> będzie dowolnym grafem. Relacją osiągalności w grafie G nazywamy relację binarną r w zbiorze wierzchołków grafu, taką że (u,v) ∈ r wttw w grafie G istnieje droga prowadząca od u do v.
Łatwo zauważyć, że relacja osiągalności jest relacją przechodnią.
Nie musi być jednak symetryczna. Mówimy, że relacja osiągalności
jest tranzytywnym domknięciem relacji sąsiedztwa w grafie.
Pytanie 3.2.3 Niech M
będzie
macierzą relacji sąsiedztwa pewnego grafu G, gdzie M(i,j)=1 wtedy i
tylko wtedy, gdy wierzchołek i-ty i wierzchołek j-ty są połączone
krawędzią, i M(i,j) = 0 w pozostałych przypadkach. Zinterpretuj
elementy
iloczynu macierzy MxM.
| « poprzedni punkt | następny punkt » |