| « poprzedni punkt | następny punkt » |
Wróćmy na chwilę do problemu Mostów Królewieckich. Można go sformułować następująco: Czy istnieje w grafie przedstawionym na rysunku Rys. 2.11b droga, przechodząca przez wszystkie krawędzie grafu, i to przez każdą tylko raz?
Drogi tego typu są nazywane od nazwiska twórcy teorii grafów - drogami Eulera.
Definicja 3.4.1
Drogą Eulera nazywamy
drogę w grafie, która przechodzi przez wszystkie krawędzie i przez
każdą dokładnie raz. Jeżeli ta droga prosta jest cyklem, to nazywamy ją
cyklem Eulera. Graf posiadający cykl Eulera nazywamy Eulerowskim.
Twierdzenie 3.4.1
Warunkiem koniecznym i dostatecznym na to, by skończony graf niezorientowany i spójny posiadał cykl Eulera jest by wszystkie wierzchołki tego grafu miały rząd parzysty.
Warunkiem koniecznym i dostatecznym na to by w grafie niezorientowanym skończonym i spójnym istniała droga Eulera łacząca wierzchołki A i B jest by jedynymi wierzchołkami rzędów nieparzystych były co najwyżej wierzchołki A i B.
Sformułowanie tego twierdzenia może się wydać trudne. Jeśli tak, to zachęcamy Czytelnika do powrotu w to miejsce, po przeczytaniu wykładu szóstego. W istocie, kryterium Eulera jest bardzo proste. Jeśli każdy wierzchołek ma rząd parzysty, to taki graf posiada cykl i drogę Eulera. Jeśli w grafie są wierzchołki rzędu nieparzystego, to albo są dokładnie dwa takie wierzchołki i wtedy istnieje łącząca je droga Eulera, albo nie istnieje żadna droga Eulera w tym grafie.
Zadanie 3.4.1
Sprawdź, w którym z grafów przedstawionych na rysunku 3.4.1 istnieje cykl lub droga Eulera. Jeśli w grafie istnieje cykl lub droga Eulera, to można ją narysować nie odrywając ołówka od papieru. Miłej Zabawy!
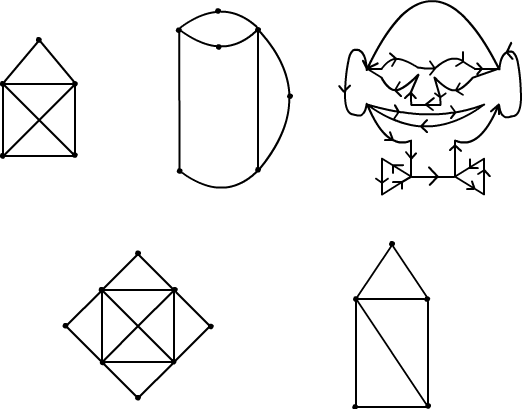
Rys. 3.4.1 Przykłady grafów.
Definicja 3.4.2
Drogą Hamiltona w
grafie G nazywamy drogę przechodzącą przez wszystkie wierzchołki grafu
i
to przez każdy wierzchołek dokładnie raz. Jeżeli droga ta jest cyklem,
to nazywamy ją cyklem Hamiltona. Graf posiadający cykl Hamiltona
nazywamy Hamiltonowskim.
Chociaż pozornie problem drogi Eulera i problem drogi Hamiltona
wydają się być dualne i podobne, to problem znalezienia drogi Hamiltona
nie
ma żadnego prostego rozwiązania. Nie jest znany żaden warunek konieczny
i dostateczny na to, by graf był Hamiltonowski. Nie jest też
znany
żaden efektywny algorytm znajdowania drogi lub cyklu Hamiltona.
Zadanie 3.4.2. Sprawdź, który z
grafów na rysunku 3.4.1 jest Hamiltonowski, a który posiada drogę
Hamiltona.
Pytanie 3.4.1 Czy graf Hamiltonowski o n wierzchołkach może
mieć mniej niż n krawędzi?
| « poprzedni punkt | następny punkt » |