Przykład 3.5.1

Wyobraźmy sobie turniej, w którym bierze udział 8 drużyn. Rozgrywki odbywają się w kolejnych rundach, w których drużyny rozgrywają mecze parami. Do następnej rundy przechodzą jedynie te drużyny, które zwyciężyły w poprzedniej rundzie. Wszystkie rozgrywki tego turnieju można przedstawić w postaci grafu, por. Rys. 3.5.1. Wierzchołki grafu (oznaczone na rysunku kolejnymi literami alfabetu) odpowiadają drużynom (ponumerowanym od 1 do 8) biorącym udział w rozgrywkach. Krawędzie wychodzące z dwóch wierzchołków x i y spotykają się w jednym wierzchołku z, tylko wtedy, gdy drużyna z odniosła zwycięstwo w meczu drużyn x i y. Na przykład, mecz drużyn 5 i 6 zakończył się zwycięstwem drużyny 6. Ostatnia runda pozwala wyłonić zwycięzcę turnieju. W naszym przykładzie zwyciężyła drużyna 6.

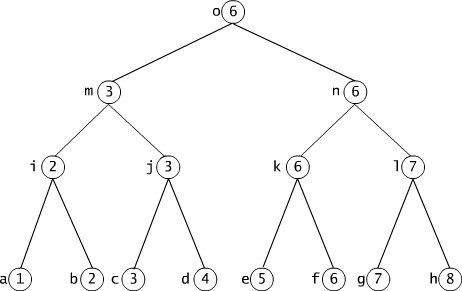
Rys. 3.5.1 Graf rozgrywek w pewnym turnieju.

Graf przedstawiony na rysunku 3.5.1 ma szczególny kształt, charakterystyczny dla pewnego typu grafów, które nie posiadają cykli, a każde dwa wierzchołki łączy tylko jedna droga.

Pytanie 3.5.1 Ile co najmniej krawędzi musi mieć graf niezorientowany o 10 wierzchołkach aby był spójny? 

W drzewie wyróżniamy zwykle jeden wierzchołek i nazywamy go korzeniem. W drzewie turnieju, przedstawionym na rysunku 3.5.1 wyróżniliśmy wierzchołek o, odpowiadający zwycięzcy turnieju. Każdy inny wierzchołek jest połączony dokładnie jedną drogą z korzeniem. Wszystkie wierzchołki znajdujące się w takiej samej odległości od korzenia tworzą w tym drzewie poziom. Na przykład wierzchołki a, b, c, d, e, f, g, h znajdują się na czwartym poziomie drzewa turnieju, a wierzchołki m, n na drugim poziomie. Jeśli dwa wierzchołki x, y są połączone krawędzią i x znajduje się na poziomie niższym (bliżej korzenia) niż y, to wierzchołek x nazywamy poprzednikiem, albo ojcem wierzchołka y, a y nazywamy następnikiem lub synem wierzchołka x. Na rysunku 2.16 wierzchołek n ma dwóch synów k i l, a wierzchołek f nie ma żadnego syna (następnika). Wierzchołki, które nie mają następników nazywa się liśćmi drzewa, a pozostałe wierzchołki - wierzchołkami wewnętrznymi.

Obserwacja W drzewie, każdy wierzchołek, z wyjątkiem korzenia, ma dokładnie jednego ojca.

Zadanie  3.5.1

Narysuj drzewo genealogiczne Twojej rodziny, tak by korzeniem tego drzewa był Twój Pradziadek. Czy jest to drzewo binarne?

Przykład 3.5.2

Każde wyrażenie arytmetyczne można przedstawić w postaci drzewa, w którym liście odpowiadają zmiennym lub stałym występującym w wyrażeniu, wierzchołki wewnętrzne wykonywanym operacjom, a krawędzie wskazują argumenty tych operacji. Na rysunku 3.5.2 przedstawiono drzewo binarne odpowiadające wyrażeniu arytmetycznemu ((x + y) * √ z). Na tym drzewie wyraźnie widać w jakiej kolejności trzeba wykonywać wskazane operacje, aby obliczyć wartość wyrażenia. Korzeniem tego drzewa jest wierzchołek z operacją mnożenia.

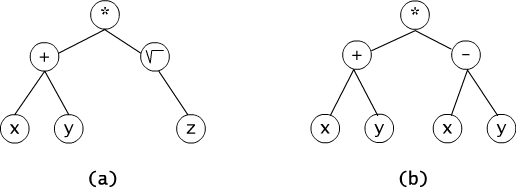
Rys. 3.5.2 Drzewo wyrażenia arytmetycznego (x + y) * √z.

Zgodnie z definicją, drzewo złożone z jednego tylko wierzchołka ma wysokość 0. Wysokość drzewa turnieju na rysunku  3.5.1 wynosi 3, a wysokość drzewa 3.5.2 wynosi 2.

Przykład 3.5.3

Drzewo na rysunku 3.5.3(b) nie jest drzewem binarnym. Przedstawia ono fragment grafu możliwych sytuacji w opisanej poniżej grze Shannona dla grafu 3.5.3(a). Na krawędziach drzewa zaznaczono możliwe ruchy graczy, tzn. dokonane wybory krawędzi.

Dany jest niezorientowany, spójny graf G i dwa wyróżnione jego wierzchołki A i B. Dwaj gracze wykonują naprzemiennie ruchy. Gracz 1, w każdym ruchu zaznacza (np.  grubą kreską) jedną z istniejących krawędzi. Gracz 2, w każdym ruchu usuwa (skreśla) jedną z krawędzi grafu, która nie była jeszcze zaznaczona przez gracza pierwszego. Celem dla gracza 1 jest zbudowanie drogi łączącej wierzchołki A i B. Celem dla gracza 2 jest uniemożliwienie graczowi 1 zbudowania tej drogi. Wygrywa gracz, który pierwszy osiągnie swój cel. Miłej zabawy.

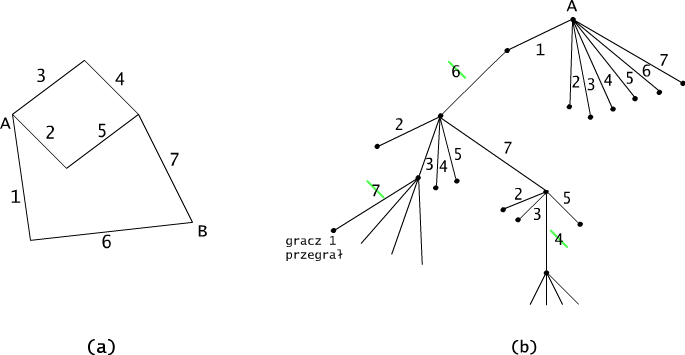
Rys. 3.5.3 Fragment grafu możliwych sytuacji w grze Shannona.

Dowód.  Na mocy definicji, jeśli G jest drzewem, to jest niezorientowanym grafem spójnym i acyklicznym. Na mocy lematu 3.3.1, G ma co najmniej n-1 krawędzi, a na mocy lematu 3.3.2 ma co najwyżej n-1 krawędzi. Zatem musi mieć dokładnie n-1 krawędzi.

Pytanie 3.5.2  Ile co najwyżej wierzchołków znajduje się w drzewie binarnym o wysokości 10?