Jeżeli każdemu elementowi zbioru X przyporządkujemy co najwyżej jeden element zbioru Y, to powiemy, że została określona funkcja w zbiorze X i o wartościach w zbiorze Y. Krótko zapisujemy ten fakt w postaci f : X → Y.

Przyporządkowanie, odwzorowanie, przekształcenie, to słowa, którymi zamiennie określa się funkcje. Jeżeli elementowi x ∈ X pewna funkcja f przyporządkowuje element y ∈ Y, to piszemy f(x) =y i element x nazywamy argumentem funkcji, a element y wartością funkcji lub obrazem elementu x.

Zbiór Dom(f) tych elementów x, którym funkcja f przypisuje wartość, nazywamy zbiorem argumentów funkcji. Zbiór Im(f) tych y, które są wartościami funkcji nazywamy zbiorem wartości funkcji.

Dom(f) = { x ∈ X : istnieje takie y ∈ Y, że f(x) = y}

Im(f) = { y ∈ Y : istnieje takie x ∈ X, że f(x) = y}

Rys. 4.1.1 (a) Przykład funkcji (b) Graf relacji, która nie jest funkcją.

Przykład 4.1.1

1. Niech S oznacza zbiór studentów PJWSTK i N zbiór liczb naturalnych. Każdy student posiada książeczkę ocen, tzw. indeks, w którym prowadzi wpisy zaliczonych przedmiotów. Odwzorowanie, które każdemu studentowi przypisuje numer jego indeksu, jest funkcją odwzorowującą S w zbiór liczb naturalnych.
2. Na rysunku 4.1.1(a) przedstawiono funkcję, która kółeczkom przypisuje kwadraciki. Samo przypisanie zaznaczone jest strzałką łączącą kółeczko z odpowiednim kwadracikiem. Zbiór argumentów tej funkcji, to zbiór kółeczek, a zbiór wartości, to zbiór kwadracików. Rysunek 4.1.1.(b) natomiast, nie przedstawia funkcji: pierwsze kółeczko ma przypisane aż dwa kwadraciki - dwie wartości. Taka niejednoznaczność nie może się zdarzyć w przypadku funkcji ( a nie przeszkadza w opisie relacji!).
3. Niech A będzie pewnym alfabetem (tzn. niepustym zbiorem), a A* zbiorem słów zapisanych w tym alfabecie. Określimy przyporządkowanie f, które słowom przypisuje ich długość (tzn. liczbę wystąpień znaków, z których składa się dane słowo). Na przykład, jeśli A składa się z liter naszego alfabetu, to f(abecadło) = 8, f(aaabbb) = 6. Funkcja f jest określona w zbiorze A* , a jej wartościami są liczby naturalne

f : A* → N

Rozważmy jeszcze jeden przykład dobrze znanej funkcji. Niech suc oznacza odwzorowanie,

suc : N → N,

które liczbie naturalnej n przypisuje jej bezpośredni następnik, suc(n) = n+1. Oczywiście, dla każdej liczby naturalnej n jest określony następnik suc(n), suc(0) = 1, suc(1) = 2, suc(2) = 3 itd. Wydaje się, że zupełnie analogicznie można danej liczbie przyporządkować jej poprzednik, definiując pred: N → N tak, że

pred(n) = n-1.

Jednak teraz sytuacja jest nieco inna. Liczbie naturalnej 1 przypiszemy 0, a co przypiszemy liczbie 0? Odwzorowanie pred nie jest określone dla liczby 0. O takiej funkcji mówimy, że jest częściowa, w przeciwieństwie do funkcji całkowitej, jaką jest następnik suc.

Z tego co do tej pory powiedzieliśmy o funkcjach wynika, że każda funkcja f : X → Y, determinuje pewien zbiór par postaci (x, f(x)) takich, że żadne dwie pary nie mają tego samego poprzednika. Takie spojrzenie na funkcje prowadzi do następującej definicji:

Przykład 4.1.2

1. Relacja binarna określona w produkcie N × N jako {(x,y) : x, y ∈ N oraz y =2n+1} jest funkcją całkowitą, która każdej liczbie naturalnej n przyporządkowuje liczbę naturalną 2n+1. Dom(f) = N, Im(f) = NP.
2. Zbiór par (x, x²) dla x ∈ R jest relacją binarną w R. Jest to funkcja, która dowolnej liczbie rzeczywistej przypisuje jej kwadrat. Dom(f) = R , Im(f) = R+ (por. Rys.2.3a)
3. Relacja r ={(x,y) ∈ R² : x² = y² } nie jest funkcją ponieważ (1,-1) ∈ r i równocześnie (1,1) ∈ r. Jeśli jednak ograniczymy relację r do zbioru liczb naturalnych przyjmując r' = {(x,y) ∈ N² : x² = y² }, to taka relacja wyznacza funkcję id : N → N, która każdej liczbie naturalnej przypisuje tę właśnie liczbę, id(n) = n dla wszystkich n ∈ N.
4. Niech A będzie dowolnie ustalonym podzbiorem pewnego zbioru X. Funkcja f : X → {0,1}, taka że f(x) = 1, gdy x ∈ A i f(x) = 0, gdy x ∉ A nazywa się funkcją charakterystyczną zbioru A. Na rysunku 3.2 przedstawiono funkcję charakterystyczną podzbioru A = [2,5] zbioru liczb rzeczywistych.

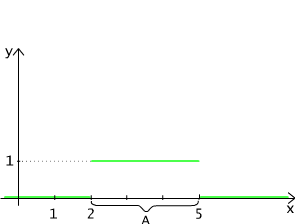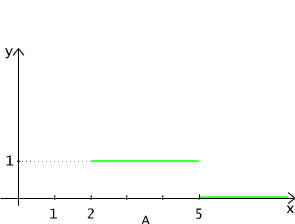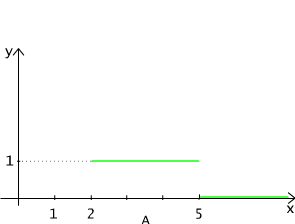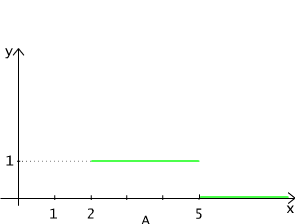
Rys. 4.1.2 Funkcja charakterystyczna przedziału [2,5] zbioru liczb rzeczywistych.

Szczególnym przypadkiem funkcji są skończone i nieskończone ciągi. Ciąg jest to funkcja określona na zbiorze liczb naturalnych N lub jakimś jego segmencie N_k (skończonym lub nie) postaci [k, k+1, k+2, k+3,..., k+i,...], gdzie k jest ustaloną liczbą naturalną, a i ∈ N. Jeśli dziedziną ciągu jest zbiór nieskończony, to mówimy o ciągu nieskończonym, w przeciwnym przypadku mówimy o ciągu skończonym.

Jeśli c : N_k → Y, to wartości funkcji c dla argumentu k+i oznaczamy c_k+i i nazywamy i-tym wyrazem ciągu c, a liczbę k+i jego indeksem. Sam ciąg zwykle zapisujemy w postaci listy (c _k, c _k+1, c_k+2, c _k+3,...) lub krócej (c _j) _{j ∈ Nk} lub, jeśli jest to ciąg skończony, w postaci (c _j) _{k ≤ j ≤ n} .

Przykład 4.1.3

1. Funkcja f : N → N taka, że f(n) = n! jest ciągiem nieskończonym o wyrazach (1, 1, 2, 6, 24, 120,...).
2. Funkcja g : N → Z określona wzorem g(n) = (-1)ⁿ jest ciągiem nieskończonym (1, -1,1,-1,1,-1,...), którego zbiór wyrazów jest dwuelementowy.
3. Funkcja h : N → N, której wyrazy określają liczbę kul w kolejnych trójkątach przedstawionych na rysunku 4.1.3 jest ciągiem postaci (1, 3, 6, 10,15,...). Zauważmy, że h(i) = 1+2+...+i = i(i+1)/2. i-ty wyraz ciągu h nazywa się i-tą liczbą trójkątną.

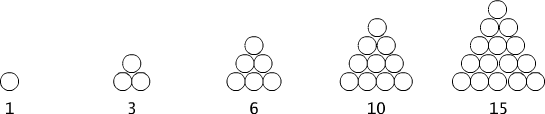
Rys. 4.1.3 Liczby trójkątne.

Funkcje, podobnie jak relacje, możemy przedstawiać w postaci grafu, wykresu lub tablicy wartości. Na rysunku 4.1.4(a) przedstawiliśmy wykres funkcji f(x) = |x|,

f(x) = x dla x ≥ 0 i f(x) = -x dla x < 0,

określonej na zbiorze liczb rzeczywistych i o wartościach nieujemnych. Na rysunku 4.1.4(b) przedstawiliśmy funkcję g, odwzorowującą zbiór liczb rzeczywistych w zbiór liczb rzeczywistych, określoną jako

g(x) = c wttw c jest najmniejszą liczbą całkowitą c ≥ x.

Dziedziną funkcji g jest zbiór liczb rzeczywistych, a przeciwdziedziną zbiór liczb całkowitych. Funkcja g jest tzw. funkcją schodkową. Funkcję tę oznaczamy symbolem ⎡x ⎤.

Na rysunku 4.1.4 (c),(d) przedstawiliśmy tablicę wartości i graf funkcji h(x) = (x+2) mod 4, której wartością jest reszta z dzielenia x+2 przez 4.

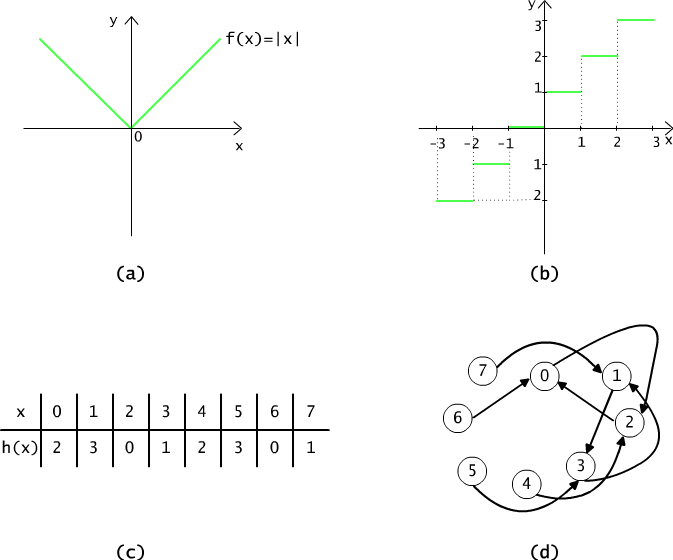
Rys. 4.1.4 (a) Wykres funkcji |x|. (b) Wykres funkcji schodkowej ⎡x ⎤ . (c) Tablica wartości funkcji (x+2) mod 4 i (d) jej graf.

Pytanie 4.1.1: Niech f(x) = 2^x będzie funkcją określoną na zbiorze {0, 1, 2, ...,10}. Jaki jest jej zbiór wartości?

Zadanie 4.1.1

Narysować wykres funkcji f(x) = c wttw gdy c jest największą liczba naturalną niewiększą niż |x| (|x| wartość bezwzględna x), dla x ∈ R.