Mówiąc w tym wykładzie o funkcjach, zwykle mieliśmy na myśli odwzorowanie f: X → Y określone w jakimś zbiorze X i nie interesowaliśmy się strukturą samego zbioru X.

Jeżeli zbiór X jest produktem kartezjańskim zbiorów X₁,..., X_n, to mówimy o n-argumentowej funkcji

f : X_{1 ×} ... × X_n → Y

odwzorowującej produkt kartezjański X_{1 ×} ... × X_n = P_{i ≤ n} X_i w zbiór Y.

Wszystkie definicje jakie przyjęliśmy w poprzednich częściach wykładu przenoszą się bez zmiany na funkcje wieloargumentowe wobec faktu, że funkcje wieloargumentowe, są szczególnym przypadkiem funkcji jednoargumentowych.

Jeżeli f(x₁,..., x_n) = y, to x_i nazywamy i-tym argumentem funkcji f.

W matematyce i w informatyce dużo mówi się o różnego rodzaju operacjach. Na przykład dodawanie liczb rzeczywistych jest operacją wykonywaną na dwóch argumentach rzeczywistych, i której wynik jest liczbą rzeczywistą. Co wiecej, parze liczb rzeczywistych przypisujemy tylko jedną liczbę rzeczywistą. Jest to więc funkcja dwuargumentowa

+ : R × R → R

Ogólnie, każda n-argumentowa operacja w zbiorze X, to n-argumentowa funkcja ze zbioru X ⁿ w X.

Przykład 4.5.1

1. Niech X będzie pewnym ustalonym uniwersum. Operacja różnicy symetrycznej zbiorów określona na podzbiorach zbioru X jest dwuargumentową funkcją, ⊕ : P(X) × P(X) → P(X), taką, że dla dowolnych A,B, ⊕ (A, B) = A\B ∪ B\A. Tradycyjnie, tak jak i w przypadku innych operacji dwuargumentowych, symbol operacji piszemy między argumentami, czyli zamiast ⊕ (A, B) piszemy A ⊕ B.
2. Niech S będzie zbiorem studentów PJWSTK. Na zakończenie studiów do indeksu wpisuje się średnią z uzyskanych ocen. Mamy tu do czynienia z funkcją n+1-argumentową, gdzie n jest liczbą zaliczanych egzaminów, która każdemu studentowi i uzyskanym przez niego ocenom ocena₁, ..., ocena_n przypisuje liczbę rzeczywistą równą (ocena₁, ..., ocena_n )/n.
3. Rozważmy teraz przykład typowo informatyczny: program. Każdy deterministyczny program P można traktować jako wieloargumentową funkcję (częściową), która danym do programu przypisuje wyniki, por. Rys. 4.5.1. Dane to układ wartości parametrów wejściowych, wyniki - to układ wartości parametrów wyjściowych. Jeśli program ma na celu obliczanie wartości wielomianu w(x) = a₀ + a₁x + ... + a_nxⁿ, dla wielu zmieniających się parametrów i dla różnych argumentów x, to warto tak go zaprojektować, by współczynniki wielomianu i wartość zmiennej były danymi do programu. Jeśli zmienną wynik potraktujemy jako tę, która przechowuje wyliczoną wartość wielomianu, to program może wyglądać następująco (algorytm Hornera)

begin wynik := a_n; i := n; while i>0 do i := i-1; wynik := wynik * x + a_i od end;

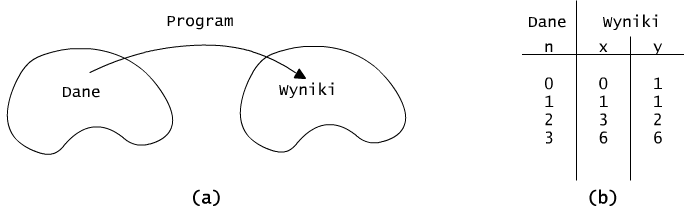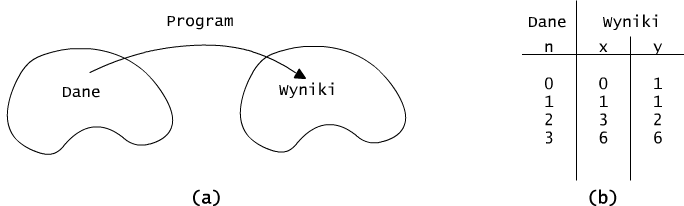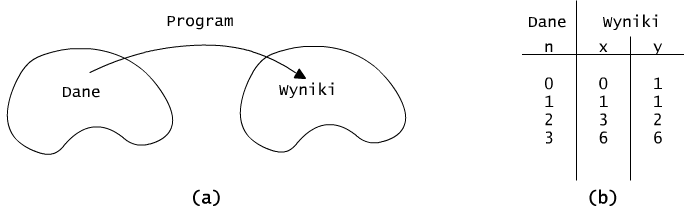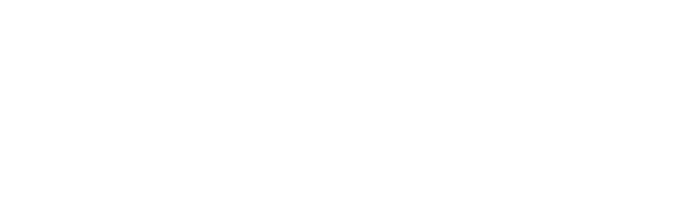
Rys. 4.5.1 Program, jako odwzorowanie przekształcające dane w wyniki.