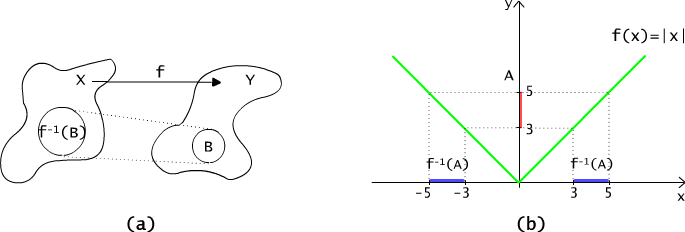
| « poprzedni punkt | następny punkt » |
Definicja 4.4.1
Obrazem zbioru A ⊆ X wyznaczonym przez funkcję f : X → Y nazywamy zbiór f(A) wartości jakie przyjmuje ta funkcja dla argumentów ze zbioru A, (por. Rys. 4.4.1(a))
f(A) = {y : istnieje x ∈ A, f(x) = y}.
Przykład 4.4.1
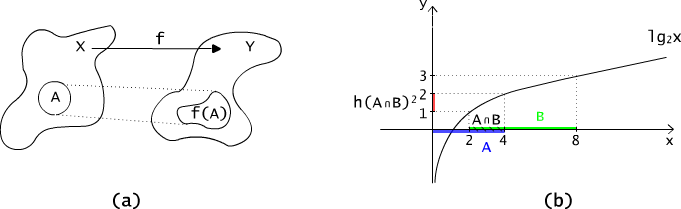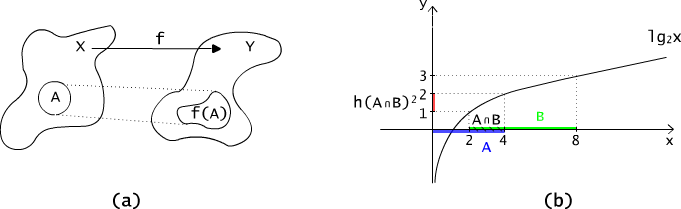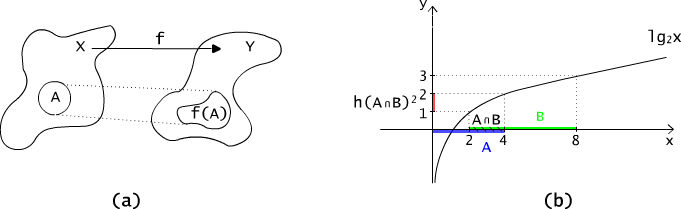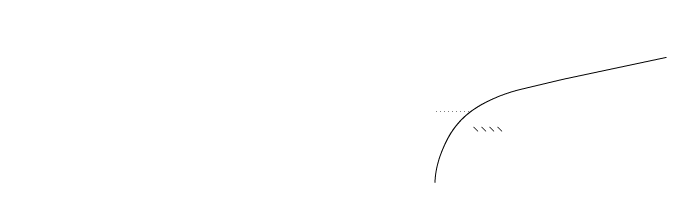
Rys. 4.4.1 Obraz zbioru otrzymany przy pomocy funkcji.
Lemat 4.4.1
Dla dowolnych zbiorów A, B ⊆ X i dla dowolnej funkcji f : X → Y,
Dowód.
Ad 1. Pierwsza z równości jest dość oczywista:
y ∈ f(A ∪ B) wttw y = f(x) dla pewnego x ∈ A ∪ B wttw x ∈ A i y =f(x) lub x ∈ B i y =f(x) wttw y ∈ f(A) lub y ∈ f(B) wttw y ∈ f(A) ∪ f(B).
Ad 2. Dowód drugiej własności jest analogiczny jeżeli y ∈ f(A ∩ B), to y = f(x) dla pewnego x ∈ A ∩ B. To z kolei pozwala wywnioskować, że dla pewnego y, x ∈ A i x ∈ B i y = f(x), a zatem y ∈ f(A) i y ∈ f(B) co jest równoważne y ∈ f(A) ∩ f(B).
Zastanówmy się jeszcze dlaczego w przypadku (2) nie ma równości. Przeanalizujmy, jeszcze raz przykłady. Dla funkcji g z przykładu 4.4.1(2), g(A ∩ B) jest zbiorem pustym, a g(A) ∩ g(B) = {0}. Natomiast dla funkcji h z przykładu 4.4.1(3) mamy: A ∩ B =[2, 4], h(A ∩ B) =[1, 2]= (- ∝ , 2] ∩ [1, 3] =[1, 2], por. Rys. 4.4.1(b).
Pytanie 4.4.1: Jaki warunek musi spełniać funkcja f, by f(A ∩ B) = f(A) ∩ f(B) dla dowolnych zbiorów A i B.
Definicja 4.4.2
Przeciwobrazem zbioru B ⊆ Y wyznaczonym przez funkcję f nazywamy zbiór f -1(B) złożony z tych argumentów funkcji f, dla których wartości należą do B, (por. Rys. 4.4.2(a)),
f -1(B) = { x ∈ X : f(x) ∈ B}.
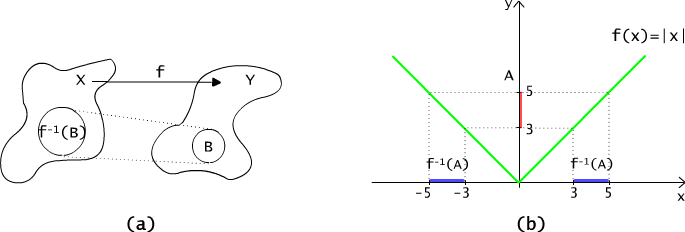
Rys. 4.4.2 Przeciwobraz zbioru wyznaczony przez funkcję.
Na rysunku 4.4.2 (b) zaznaczono przeciwobraz zbioru [3, 5] dla funkcji |x|. Przeciwobrazy pewnych zbiorów wyznaczone przez funkcje z przykładu 4.4.1 przedstawiamy poniżej.
Lemat 4.4.2
Dla dowolnych zbiorów A,B ⊆ Y i dowolnej funkcji f : X → Y,
Dowód w obu przypadkach jest bardzo podobny. Przedstawimy dla przykładu uzasadnienie wzoru (2):
x ∈ f -1 (A ∩ B) wttw f(x) ∈ (A ∩ B) wttw f(x) ∈ A i f(x) ∈ B wttw x ∈ f -1(A) i x ∈ f -1(B) wttw x ∈ f -1 (A) ∩ f -1 (B).
Pytanie 4.4.1: Niech f : R → R, będzie funkcją określoną wzorem f(x) = x 2 -5x + 4. Wyznaczyć f(R\R+ ) oraz f -1 ( {0,4}).
Zobacz odpowiedź
| « poprzedni punkt | następny punkt » |