W tym paragrafie przedstawimy zastosowanie zasady abstrakcji do konstrukcji liczb całkowitych i wymiernych.

Przykład 5.6.1

Niech ∼ będzie relacją binarną w N × N, określoną dla dowolnych m, n, k, l ∈ N warunkiem

(m,n) ∼ (k,l) wttw m+l = n+k

Relacja ∼ jest zwrotna, bo dla dowolnych n, m ∈ N, m+n =n+m (dodawanie jest przemienne).

Relacja ∼ jest symetryczna, bo dla dowolnych par (m,n) i (k,l), jeśli (m,n) ∼ (k,l), to m+l = n+k, a zatem (z przemienności dodawania) k+n = m+l, czyli (k,l) ∼ (m,n).

Ponadto relacja ∼ jest przechodnia, bo jeśli (m,n) ∼ (k,l) i (k,l) ∼ (u,w), to m+l = n+k oraz k+w = l+u, co, po dodaniu stronami i zastosowaniu prawa łączności dla dodawania. daje m+(l + k)+w = n+(k + l)+u, a po uproszczeniu m+w = n+u, czyli (m,n) ∼ (u,w).

Wszystkie pary liczb (m, n), dla których różnica m-n jest taka sama należą do tej samej klasy abstrakcji (por. Rys. 4.5). Klasa [(0, 0)] to zbiór par o identycznym poprzedniku i następniku, np. (1,1), (3,3), (100,100) ∈ [(0,0)]. Wspólną cechą par (m,n) ∈ [(0,0)] jest to, że m-n=0. Do klasy [(1,0)] należą np. pary (7,6), (4,3), (100,99). Wspólną cechą par (m,n) ∈ [(1,0)] jest to, że m-n=1. Klasy abstrakcji relacji ∼ wyznaczają w ten sposób liczby całkowite.

• Jeśli m>n, to istnieje k ∈ N takie, że n+k=m. Cechę charakterystyczną dla klasy [(m,n)], gdy m>n, nazywamy liczbą całkowitą dodatnią i oznaczamy przez +k.

• Jeśli m<n, to istnieje k ∈ N takie, że m+k=n. Cechę charakterystyczną dla klasy [(m,n)], gdy m<n, nazywamy liczbą ujemną i oznaczamy przez -k.

• Jeśli m=n, to klasa [(m,n)] wyznacza liczbę całkowitą 0.

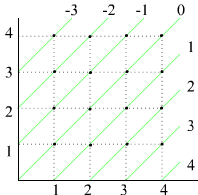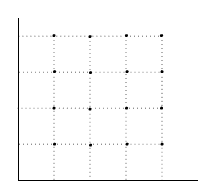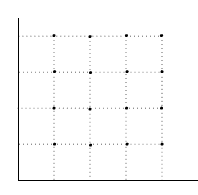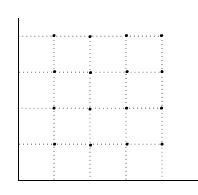
Rys. 5.6.1 Klasy abstrakcji relacji równoważności określonej w zbiorze N × N (por. przykład 5.6.1).

Pytanie 5.6.1: Rozważmy klasy abstrakcji w sensie relacji z przykładu 4.7. Czy [(5,8)] = [(1,4)]?

Definicja liczb całkowitych podana w przykładzie 4.7 to nie wszystko. Podobnie jak na liczbach naturalnych, chcemy na liczbach całkowitych wykonywać operacje dodawania mnożenia lub odejmowania. Jeśli rzeczywiście klasy abstrakcji mają odpowiadać liczbom całkowitym musimy umieć wykonywać na nich operacje arytmetyczne. Okazuje się, że w zbiorze klas abstrakcji relacji ∼ można określić w sposób naturalny operacje + i *, które mają wszystkie te własności, których spodziewamy się po znanych nam operacjach na liczbach całkowitych. Oto definicje tych operacji:

dla dowolnych liczb naturalnych m, n, k, l.

Chociaż symbole operacji po lewej i po prawej stronie powyższych równości są takie same, to te po lewej są symbolami definiowanych operacji, a te po prawej stronie symbolu = ^df są znanymi operacjami dodawania i mnożenia w zbiorze liczb naturalnych.

Sprawdźmy dla przykładu, czy w zdefiniowanej arytmetyce (+2) + (-3) = -1? Liczba całkowita +2 jest reprezentowana przez klasę [(2,0)] wyznaczoną np. przez uporządkowaną parę liczb naturalnych (2,0) (ale jej reprezentantem może być równie dobrze para (6,4) albo (15,13)). Liczba całkowita -3 jest reprezentowana przez klasę [(0,3)], a liczba całkowita -1 przez klasę [(0,1)]. Policzmy

(+2) + (-3) = [(2,0)] + [(0,3)] = [(2+0, 0+3)] = [(2,3)] = [(0,1)] = -1.

Zauważmy, że wybór reprezentantów klas abstrakcji nie ma wpływu na wynik wykonywanych operacji, bo mamy

(+2) + (-3) = [(15,13)] + [(4,7)] = [(15+4, 13+7)] = [(19,20)] = [(0,1)] = -1.

Pytanie 5.6.2: Jaki jest wynik mnożenia liczb całkowitych reprezentowanych przez klasy abstrakcji [(5,2)], [(1,4)]?

Zadanie 5.6.1

Określ na klasach abstrakcji relacji ∼ z przykładu 4.7 operację odejmowania liczb całkowitych.

Rozwiązanie [(m,n)] - [(k,l)] = ^df [(m+l, n+k)].

Przykład 5.6.2

Niech Z oznacza zbiór liczb całkowitych i niech ∼ będzie relacją binarną określoną w produkcie Z × Z\{0} następująco:

(m, n) ∼ (k, l) wttw m*l = n*k

Relacja ∼ jest zwrotna, bo m*n = n*m, a więc (m, n) ∼ (m, n).

Relacja ∼ jest symetryczna, bo jeśli (m, n) ∼ (k, l), to m*l = n*k, a więc również k*n = l*m, na mocy przemienności mnożenia w zbiorze liczb naturalnych, czyli (k, l) ∼ (m, n).

Relacja ∼ jest przechodnia. Załóżmy, że (m, n) ∼ (k, l) i (k, l) ∼ (u, w), wtedy, na mocy definicji, mamy m*l = n*k i k*w = l*u, co po pomnożeniu stronami daje m*(l*k)*w = n *(k*l)*u. Jeśli k ≠ 0, to ponieważ (k*l) jest wtedy liczbą różną od zera, więc (po podzieleniu) mamy m*w = n *u, czyli (m, n) ∼ (u, v). Jeśli k=0, to m*l = 0 i 0 = l*u, a stąd (ponieważ l ∈ Z\{0}) musi być m= u = 0 i w konsekwencji (m, n) ∼ (u, v).

W ten sposób udowodniliśmy, że ∼ jest relacją równoważności.

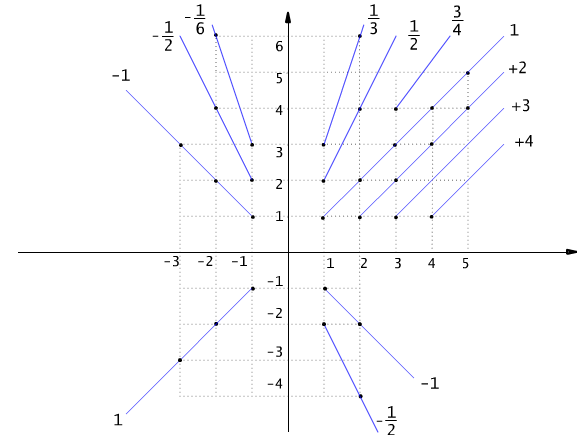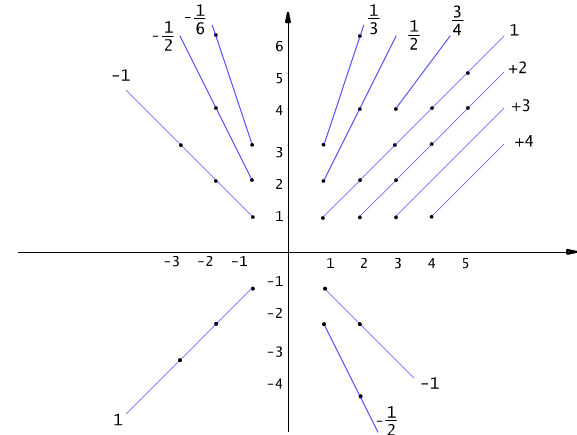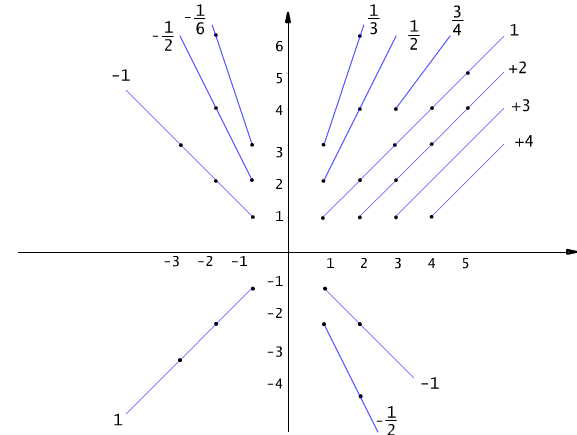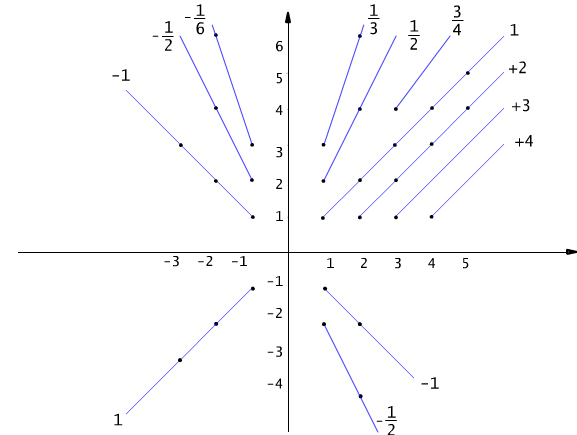
Rys. 5.6.2 Klasy abstrakcji relacji równoważności określonej w zbiorze Z × Z\{0} (por. przykład 5.6.2).

Zauważmy, że wszystkie pary postaci (m,n) należące do tej samej klasy abstrakcji mają tę samą wartość ilorazu m/n (por. Rys. 5.6.2). Na przykład pary (2,4), (3,6), (5,10), (15,30) są ze sobą w relacji i wszystkie należą do klasy abstrakcji [(1,2)]. Przypiszmy tej klasie liczbę wymierną 1/2. Ogólnie, klasa abstrakcji [(m,n)] wyznacza liczbę wymierną m/n.

Podobnie jak w przykładzie poprzednim, na klasach abstrakcji relacji określonej w przykładzie 4.8 możemy zdefiniować operacje arytmetyczne, odpowiadające operacjom na liczbach wymiernych. Przyjmujemy

dla dowolnych liczb całkowitych m, k ∈ Z i n, l ∈ Z\{0}.

Operacje + i * występujące po lewej stronie powyższych równości definiujemy za pomocą odpowiadających im działań w zbiorze liczb całkowitych. Można udowodnić, że wszystkie prawa arytmetyki liczb wymiernych przysługują operacjom +, * zdefiniowanym na klasach abstrakcji relacji ∼ .

Pytanie 12: Rozważmy relację omawianą w przykładzie 4.8. Jaka jest wartość wyrażenia [(3,4)] + [(1,8)]?

Przykład 5.6.3

Niech R^{+ N} oznacza zbiór wszystkich funkcji f: N → R⁺ i niech ∼ będzie relacją binarną w tym zbiorze taką, że dla dowolnych funkcji f, g ∈ R^{+ N},

f ∼ g wttw istnieją dodatnie stałe rzeczywiste c₁, c₂, n₀, takie że g(n) ≤c₁f(n) i c₂f(n) ≤g(n) dla wszystkich n > n₀.

Relacja ∼ jest relacją równoważności. Zwrotność i symetria wynikają natychmiast z definicji. Dla dowodu przechodniości załóżmy, że f ∼ g i g ∼ h. Wtedy istnieją stałe c₁, c₂, n₀ oraz c₁', c₂', n₀', że spełnione są nierówności

Stąd dla wszystkich liczb naturalnych n większych od większej z liczb n_{0 ,} n₀' mamy

a to oznacza, że f ∼ h.

Klasę abstrakcji tej relacji [f] wyznaczoną przez funkcję f oznacza się symbolem Θ (f). Funkcje n + lg n + n², 2n+(n+7) ²+100, (n⁵ + 3)/(n³-1), 2 ^{2lg n} należą do tej samej klasy abstrakcji relacji ∼ , a mianowicie do [n²]. Natomiast, każda z funkcji lg n, n, nlgn, n², n³, 2ⁿ, 3ⁿ , nⁿ należy do innej klasy abstrakcji.

O funkcjach należących do tej samej klasy abstrakcji relacji ∼ mówimy, że mają ten sam rząd (por. punkt 4.6).

Przykład 5.6.4

Niech S będzie zbiorem studentów PJWSTK i niech rs będzie funkcją rs : S → N, która każdemu studentowi przypisuje rok, na którym aktualnie studiuje. Wartościami funkcji rs są więc liczby 1, 2, 3, 4, 5. W zbiorze S określimy teraz relację binarną ∼ : dla dowolnych s', s" ∈ S, s' ∼ s" wttw rs(s') = rs(s").

Zgodnie z lematem 5.1.1, relacja ta jest relacją równoważności. Klasami abstrakcji tej relacji są grupy studentów tworzące dany rok studiów. Jeśli Jan Kowalski jest studentem 1-go roku PJWSTK, to

[Jan Kowalski] = zbiór wszystkich studentów studiujących na pierwszym roku PJWSTK.

Mamy więc dokładnie 5 klas abstrakcji rozważanej relacji.

Plan zajęć układany jest oczywiście dla wszystkich studentów Uczelni, ale nie układa się planu zajęć dla każdego studenta z osobna (wyobraźmy sobie jaka byłaby to skomplikowana praca), i nie ma potrzeby wypisywania planu dla każdego. Wystarczy ułożyć plan zajęć dla pierwszego, drugiego, itd. piątego roku. Student Jan Premier zapozna się ze swoim planem oglądając plan dla pierwszego roku, a studentka piątego roku Anna Derniere zapozna się ze swoim planem oglądając plan 5-tego roku. Proste.

Jeśli pan Rektor zechce przyznać nagrodę wszystkim studentom pierwszego roku za doskonałe wyniki w nauce, to wystarczy jeśli napisze jedno ogłoszenie zaadresowane do studentów pierwszego roku, a nie 290 takich ogłoszeń do poszczególnych studentów pierwszego roku.