Relacje porządku zwykle będziemy oznaczać symbolem ≤ . Zbiór, w którym określona jest relacja porządku nazywamy uporządkowanym, co zapisujemy <X, ≤ >. Jeśli chcemy zaznaczyć, że relacja ≤ zachodzi między elementami x i y, ale są one różne, to piszemy x ≤ y, podobnie jak to czynimy w przypadku relacji ≤ w zbiorze R.

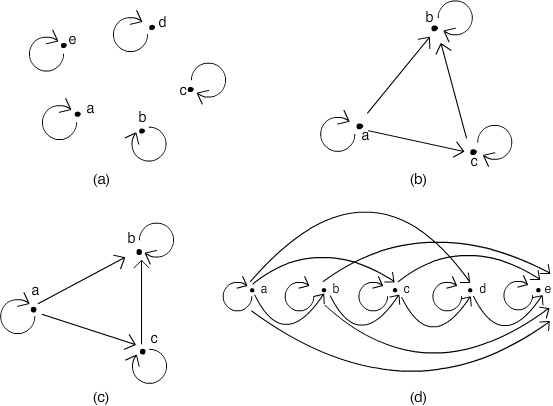
Rys. 6.1.1 Przykłady zbiorów częściowo uporządkowanych.

Na rysunku 6.1.1 przedstawiliśmy przykłady grafów ilustrujących pewne zbiory uporządkowane. Graf na rysunku 6.1.1(a) przedstawia relację porządku częściowego. Jest to oczywiście relacja zwrotna, ale jest też antysymetryczna i przechodnia. Nie zachodzi dla żadnej pary różnych elementów, a zatem implikacje (2), (3) są prawdziwe. Graf na rysunku 6.1.1(b) przedstawia także relację porządku. Tu jednak, w przeciwieństwie do 6.1.1(a), potrafimy porównać niektóre różne elementy: a ≤ b i a ≤ c. Relacja przedstawiona na rysunku 6.1.1(c), pozwala ustawić wszystkie elementy w ciąg a ≤ c ≤ b. Podobnie w przypadku grafu 6.1.1(d), gdzie każde dwa elementy można ze sobą porównać.

Pytanie 6.1.1: Czy graf pełny jest ilustracją zbioru uporządkowanego?

Przykład 6.1.1

1. Jako pierwszy przykład relacji porządku weźmy relację ≤ w zbiorze liczb rzeczywistych. Oczywiście dla dowolnych liczb rzeczywistych x, y, z ∈ R mamy x ≤ x, jeśli x ≤ y i y ≤ x, to x = y, jeśli x ≤ y i y ≤ z, to x ≤ z. Wynika stąd również, że zbiory liczb naturalnych N, liczb wymiernych Q, liczb całkowitych Z są uporządkowane przez relację ≤ .
2. Relacja ≤ określona w zbiorze wszystkich funkcji z R w R, R^R, taka że dla f, g ∈ R^R

   f ≤ g wttw dla dowolnego x ∈ R, f(x) ≤ g(x),

   jest relacją porządku w R^R. Rzeczywiście, f(x) ≤ f(x) dla dowolnego x ∈ R, czyli ≤ jest zwrotna. Niech f ≤ g i g ≤ f i niech x będzie ustaloną liczbą rzeczywistą. Ponieważ, na mocy pierwszego założenia, f(x) ≤ g(x) oraz g(x) ≤ f(x) na mocy drugiego założenia, to z antysymetrii relacji ≤ mamy f(x)=g(x). Rozumowanie to można powtórzyć dla wszystkich x ∈ R, dowodząc tym samym, że dla każdego x ∈ R, f(x) = g(x). Czyli f = g. Dla dowodu przechodniości relacji ≤ załóżmy, że f ≤ g i g ≤ h. Weźmy dowolną liczbę rzeczywistą x. Na mocy założeń mamy f(x) ≤ g(x) i g(x) ≤ h(x). Korzystając teraz z przechodniości relacji ≤ , otrzymujemy f(x) ≤ h(x). Powtarzając to samo rozumowanie dla wszystkich x ∈ R dojdziemy do wniosku, że f ≤ h.
   Zatem relacja ≤ jest przechodnia, co kończy dowód, że ≤ jest również relacją porządku.
3. Relacja przedstawiona w poprzednim przykładzie wykorzystywała w istotny sposób własności relacji ≤ w zbiorze liczb rzeczywistych. Może się wydawać, że użycie relacji ≤ w definicji wystarcza aby nowa relacja była porządkiem. Tak jednak nie jest. Rozważmy relację r określoną w zbiorze funkcji R^+N, taką że

   f r g wttw istnieją dodatnie stałe c i n₀, że f(n) ≤ c*g(n) dla n > n₀.

   Zgodnie z naszą definicją, funkcje f i g są w relacji r, jeśli f = O(g), tzn. g szacuje z góry funkcję f (por. punkt 4.6). Tak zdefiniowana relacja jest zwrotna i przechodnia, ale nie jest antysytmetryczna. Niech f(n) = 2n i g(n) = 5n. Wtedy dla wszystkich n mamy f(n) ≤ g(n) oraz dla wszystkich n ∈ N, g(n) ≤ 5 f(n). Wynika stąd, że f = O(g) i g = O(f), mimo że f i g nie są równe (f ≠ g).

Pytanie 6.1.1: Czy relacja mniejszości < w zbiorze liczb rzeczywistych jest relacją porządku?

« poprzedni punkt

następny punkt »