| « poprzedni punkt | następny punkt » |
Relacje porządku, tak jak inne relacje, można ilustrować za pomocą grafów. Jednak zwykle duża liczba krawędzi i występujące pętle (jako konsekwencja zwrotności i przechodniości) sprawiają, że rysunek taki nie zawsze jest czytelny. Wygodnym sposobem przedstawiania porządku są natomiast diagramy Hassego.
Definicja 6.2.1
Diagramem Hassego relacji porządku ≤ w zbiorze X nazywamy graf niezorientowany G = <X, E>, którego zbiorem wierzchołków jest zbiór X , a krawędzie są określone następująco
(x,y) ∈ E
wttw x ≤y i nie istnieje z ∈X, że z ≠x, z ≠y i x ≤ z i z
≤ y
Jeśli para (x,y) tworzy krawędź w diagramie Hassego, to mówimy, że y jest bezpośrednim następnikiem x.
Zwykle, zamiast strzałek łączących wierzchołki w grafie zorientowanym, w diagramach Hassego krawędzie zaznaczamy odcinkami, w taki sposób, by koniec krawędzi znajdował się na rysunku powyżej początku krawędzi.

Rys. 6.2.1 Diagram Hassego (a) relacji inkluzji w zbiorze wszystkich podzbiorów zbioru{R, G, B}, (b) relacji podzielności w zbiorze {1,2,3...9}.
Przykład 6.2.1
(1) Relacja ⊆ inkluzji w zbiorze wszystkich podzbiorów pewnego zbioru X jest relacją porządku częściowego. Oczywiście jest zwrotna, bo A ⊆ A. Jest też antysymetryczna, ponieważ A ⊆ B i B ⊆ A implikuje A = B. Relacja jest też przechodnia, bo z założeń A ⊆ B i B ⊆ C wynika natychmiast A ⊆ C (por. punkt 1.2).
Zauważmy, że nie wszystkie zbiory należące do P(X) dają się porównać za pomocą relacji ⊆. Jeśli x i y są różnymi elementami zbioru X, to mamy {x} ∈ P(X), {y} ∈ P(X), ale ani nie zachodzi {x} ⊆ {y}, ani nie zachodzi {y} ⊆ {x}.
Diagram Hassego relacji ⊆ w przypadku, gdy X = {R,G,B} przedstawiono na rysunku 6.2.1(a).
(2) Relacja podzielności | określona w zbiorze liczb naturalnych
x|y wttw x jest dzielnikiem y
jest relacją porządku. Rzeczywiście, relacja podzielności jest zwrotna, antysymetryczna i przechodnia. Na rysunku 2.2.5(b) przedstawiono graf tej relacji ograniczonej tylko do zbioru {1, 2, 3, ...9}. Rysunek 6.2.1(b) przedstawia diagram Hassego tej relacji. Podobnie jak w poprzednim przykładzie, istnieją takie liczby naturalne, których nie możemy porównać za pomocą |. Na przykład 2 nie jest dzielnikiem 3 i 3 nie jest dzielnikiem 2.
(3) Niech Σ = {0, 1}. W zbiorze Σ* zdefiniujemy relację ≤ następująco:
w ≤ w' wttw istnieje słowo w" ∈ Σ*, że ww" = w'.
Słowo ww" zostało utworzone ze słowa w przez dopisanie na jego końcu słowa w". Taką operacje na słowach nazywamy konkatenacją. Na przykład, konkatenacja słów "para" i "lotnia" daje słowo "paralotnia".
Jeżeli w' ≤ w, to mówimy, że w' jest segmentem początkowym lub prefiksem słowa w. Relacja ≤ w zbiorze {0,1}* definiuje porządek częściowy. Diagram Hassego tego porządku, z konieczności ograniczyliśmy do kilkunastu elementów, por Rys. 6.2.2. Sam zbiór {0,1}* jest przecież nieskończony.
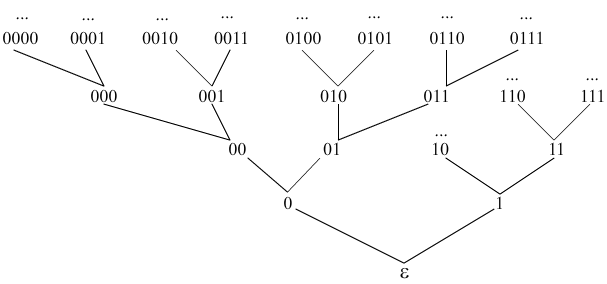
Rys. 6.2.2 Fragment diagramu Hassego relacji częściowego porządku w zbiorze słów na alfabetem {0,1}, por. przykład 6.2.1(3).
Uwaga.
Pytanie 6.2.1: Czy istnieje diagram Hassego dla zbioru uporządkowanego <Q, ≤ >?
Zobacz odpowiedź
| « poprzedni punkt | następny punkt » |