| « poprzedni punkt | następny punkt » |
Dowolny porządek ≤ w zbiorze X pozwala zdefiniować relację porządku w zbiorze par, trójek, i ogólnie n-tek elementów z X. Przyjmijmy dla dowolnych x1, x2,...xn, y1, y2,...yn ∈ X,
(x1, x2,...xn ) ≤ (y1, y2,...yn) wttw dla wszystkich i ≤ n , xi ≤ yi.
Rzeczywiście, tak określona relacja jest porządkiem częściowym w Xn. Nazywamy ją porządkiem produktowym.
Pytanie 6.6.1 W porządku produktowym na Σ4, gdzie Σ oznacza alfabet języka polskiego, który z ciągów jest wcześniejszy (P,J,W,S,T,K) czy (U,W,W,U,U,W)?
W szczególnym przypadku, gdy jako X weźmiemy zbiór liczb naturalnych N z porządkiem ≤ oraz przyjmiemy n=3, relacja ≤ porządkuje trójki liczb naturalnych. Fragment diagramu Hassego tej relacji przedstawiliśmy na rysunku 6.6.1.
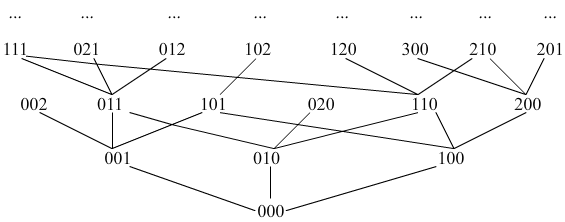
Rys. 6.6.1 Fragment diagramu Hassego porządku produktowego w zbiorze N × N × N.
Jest oczywiste, że taki porządek nie jest liniowy: chociaż trójki (5,4,3) i (2,3,8) są różne, to nie zachodzi ani (5,4,3) ≤ (2,3,8) ani (2,3,8) ≤ (5,4,3).
Czy można, bazując na jakimś danym porządku liniowym w zbiorze X, określić porządek liniowy w zbiorze Xn ?
Wróćmy znów do liczb naturalnych. Gdy n=2, łatwo możemy określić porządek liniowy wśród par liczb naturalnych, wykorzystując funkcję pary f(n, m)= n + (n+m)*(m+n+1)/2 (por. przykład 4.2.1(3)) oraz zwykły porządek ≤ w N następująco:
(n, m) ≤ (x, y) wttw f(n, m) ≤ f(x, y).
Tak określona relacja jest spójna zwrotna i przechodnia, co wynika natychmiast z odpowiednich własności dla relacji ≤ w zbiorze liczb naturalnych. Antysymetria relacji ≤ wynika z faktu, że f jest funkcją różnowartościową, tzn. (n, m) ≠ (x, y) implikuje f(n, m) ≠ f(x, y). Jeśli (n, m) ≤ (x, y) i (x, y) ≤ (n, m), to f(n, m) ≤ f(x, y) i f(x, y) ≤ f(n, m). W konsekwencji f(n, m) = f(x, y), a zatem z różnowartościowości funkcji f, (x, y) = (n, m).
Nie zawsze jednak mamy do czynienia z liczbami naturalnymi, co więcej, czasami chcemy uporządkować n-tki obiektów dla n>2. Często obiekty występujące w n-tce nie zależą do tego samego zbioru, np. jedne są liczbami, inne literami, a jeszcze inne słowami. Jak wówczas uporządkować liniowo taki zbiór? Odpowiedzią jest porządek leksykograficzny.
Definicja 6.6.1
Niech < Xi , ≤ i > dla i =1,...,n, będą zbiorami uporządkowanymi. W produkcie X1 × X2 × X3 ... × Xn określimy relację binarną ≤* następująco
(x1, x2,...xn ) ≤* (y1, y2,...yn) wttw albo dla wszystkich i ≤ n , xi = yi
albo istnieje takie 0<k ≤n, że dla 0<i<k , xi = yi oraz xk ≤ k yk, xk ≠ yk
Tak zdefiniowana relacja, nazywa się porządkiem słownikowym w X1 × X2 × ... × Xn.
Lemat 6.6.1
Jeżeli dla wszystkich i ∈ I, < Xi, ≤ i > jest zbiorem uporządkowanym, to ≤* jest porządkiem częściowym w produkcie X1 × X2 × ... × Xn. Jeśli wszystkie zbiory < Xi, ≤ i > dla i ∈ I, są liniowo uporządkowane, to relacja ≤* liniowo porządkuje zbiór X1 × X2 × ... × Xn.
Przykład 6.6.1
Jeśli X1 = X3 = {1, 2,... 9}, X2 = {a, b, ...z} z naturalnymi relacjami liniowego porządku w zbiorze cyfr i zbiorze liter alfabetu, to relacja ≤* porządkuje liniowo trójki postaci (cyfra, litera, cyfra), w taki sposób że (3,b,2) ≤* (3,c,1) ≤* (5,a,2) itd.
Dla nikogo nie jest tajemnicą, że porządek liter w alfabecie pozwala zdefiniować porządek w zbiorze słów nad tym alfabetem: porządek taki spotykamy w każdym słowniku. Jeśli rozważymy tylko słowa o ustalonej długości, to porządek słów indukowany przez porządek alfabetyczny jest zgodny ze zdefiniowanym wyżej porządkiem ≤*:
kajak ≤* kojec ≤* kolec ≤* pokaz
Słowa występujące w słowniku mają na ogół różne długości. Aby móc je miedzy sobą porównywać wprowadzimy pewne rozszerzenie relacji ≤* , oznaczone symbolem ≤ L.
Definicja 6.6.2
Niech Σ będzie ustalonym alfabetem uporządkowanym liniowo przez relację ≤. W zbiorze Σ* definiujemy relację ≤ L , porządku leksykograficznego, następująco
(x1, x2,...xn ) ≤ L (y1, y2,...ym) wttw albo n ≤ m i dla wszystkich 0<i ≤ n , xi = yi albo istnieje takie 0<k ≤min(n,m), że dla każdego i, 0< i<k, xi = yi oraz xk ≤k yk, xk ≠ yk.
Lemat 6.6.2
Relacja porządku leksykograficznego ≤L, określona powyżej, jest liniowym porządkiem w Σ*.
Pytanie 6.6.1: Co jest wcześniejsze "kura" czy "jajko" w porządku leksykograficznym ≤ L?
| « poprzedni punkt | następny punkt » |