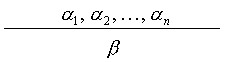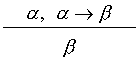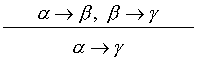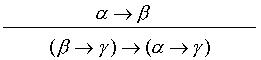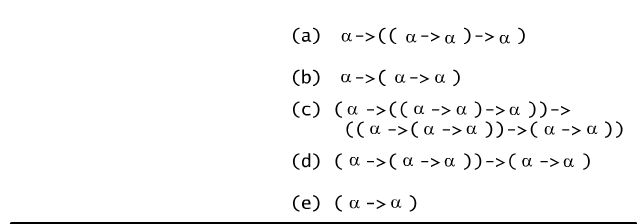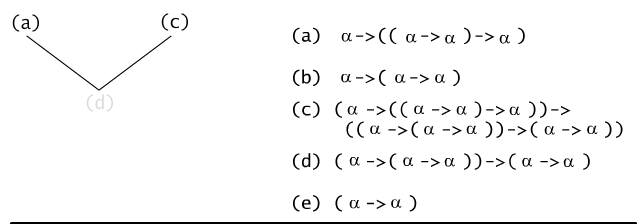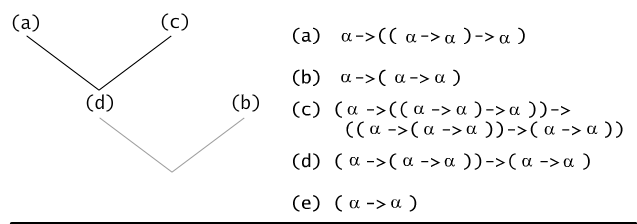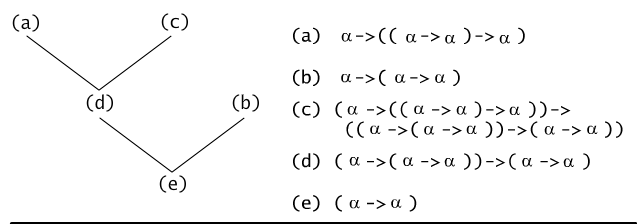Naczelnym zadaniem Rachunku Zdań jest analiza rozumowań dedukcyjnych. Na czym polega takie rozumowanie? Zaczynamy od zdań już wcześniej udowodnionych lub ogólnie przyjmowanych za prawdziwe i staramy się za pomocą prostych przekształceń doprowadzić do uzasadnienia innych zdań.

Przykład 7.6.1

Przyjmijmy, że następujące dwa zdania są prawdziwe

1. Lubię Kasię lub lubię Basię.
2. Jeśli nie lubię Kasi, to nie lubię Basi.

Czy stąd wynika koniecznie, że lubię Kasię, czy też koniecznie wynika, że lubię Basię?

Przeanalizujmy opisaną sytuację. Niech p = "Lubię Kasię ", a q = "Lubię Basię". W opisanej sytuacji oba zdania (p ∨ q) i ( ¬p ⇒ ¬ q) są prawdziwe, czyli

Gdyby w(p) =0, to w(q)=1, na mocy pierwszego założenia (a), ale wtedy w(q ⇒ p) = 0, wbrew drugiemu założeniu (b). Z prawdziwości zdań (a) i (b) wynika więc, że musi być prawdziwe zdanie "Lubię Kasię." Zdanie q natomiast nie musi być prawdziwe.

Przykład 7.6.2

Przypuśćmy, że ktoś zapytał mnie:

"Czy to prawda, że jeśli ty lubisz Kasię, to lubisz także Basię?"

Odpowiedziałam :
"Jeżeli to prawda, to lubię Kasię ".

Czy z tej rozmowy można wywnioskować, że lubię Kasię?

Przyjmijmy oznaczenia, tak jak w poprzednim przykładzie. Przedstawioną sytuację możemy krótko zapisać jako w((p ⇒ q) ⇒ p) = 1. Gdyby w przyjętej interpretacji w(p) = 0, to mielibyśmy w(p ⇒ q) = 1, ale wtedy byłoby w((p ⇒ q) ⇒ p) = 0, wbrew założeniu. Zatem odpowiedź na postawione pytanie jest twierdząca: tak, lubię Kasię. ♦

W podanych przykładach, aby wyciągnąć ostateczny wniosek z przyjętych założeń, analizowaliśmy różne sytuacje starając się ustalić, czy mogą one zaistnieć, czy też nie. Reguły wnioskowania są ogólnymi schematami postępowania formalnego, które pozwalają wyciągać wnioski, bez każdorazowego odwoływania się do semantyki i do konkretnej interpretacji.

Definicja 7.6.1

Regułą dowodzenia (inaczej zwaną regułą wnioskowania) nazywamy przekształcenie postaci

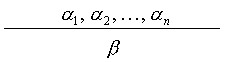
które skończonemu zbiorowi formuł α ₁, ..., α _n, zwanych przesłankami, przyporządkowuje formułę β zwaną wnioskiem, w taki sposób, że przy dowolnie wybranych wartościach zmiennych występujących w formułach α ₁,..., α _n, β , jeśli przesłanki są zdaniami prawdziwymi, to wniosek też jest zdaniem prawdziwym. Będziemy wtedy mówili, że β jest logiczną konsekwencją formuł α ₁,..., α _n .

Przykładem reguły wnioskowania jest reguła odrywania (modus ponens, m.p.):

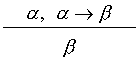
Sprawdźmy poprawność tej reguły. Niech w( α ) = 1 oraz w( α _→ β ) =1 przy pewnych ustalonych wartościach zmiennych występujących w α i β . Zgodnie z definicją funktora implikacji oraz wiedząc, że w( α ) = 1, otrzymujemy w( β ) =1. ♦

Innym przykładem jest reguła sylogizmu warunkowego

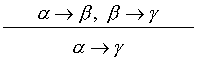
Udowodnimy, że jest to poprawna reguła dowodzenia. Przyjmijmy, że przy pewnym wartościowaniu zmiennych występujących w formułach α , β, γg mamy w( α → β )=1 oraz w( β → γ) =1 . Rozważmy dwa przypadki

1. w(α) =1. Wtedy w(β) = 1. Zatem z drugiego założenia w(γ) = 1, ale wtedy również
   w( α → γ)=1.
2. w(α) = 0. Wtedy niezależnie od wartości βoraz γ mamy również w( α → γ) = 1. ♦

Naszym trzecim przykładem reguły dowodzenia niech będzie schemat postępowania zastosowany w dowodach przez sprowadzanie do sprzeczności.

Rzeczywiście jest to poprawna reguła dowodzenia, bo przyjmując, że w( ¬ α → ( β ∧ ¬ β))=1 musimy założyć, że w( ¬ α )=0 . Stąd zaś wynika, że w( α )=1. ♦

Pytanie 7.6.1: Czy następujący schemat jest poprawną regułą dowodzenia.

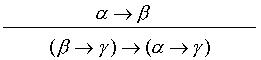Zobacz odpowiedź

Zadanie 7.6.1

Pewien kraj jest w całości zamieszkały przez ludzi, z których jedni zawsze kłamią, a inni zawsze mówią prawdę. Co więcej, małomówni tubylcy odpowiadają na każde pytanie krótko TAK lub NIE. Pewien głodny turysta doszedł do rozwidlenia dróg, z których jedna prowadziła w prawo, a druga w lewo, ale tylko jedna z nich prowadziła do restauracji. Ponieważ nie było żadnej innej wskazówki, którą drogę wybrać, turysta postanowił zapytać przechodzącego tubylca. Jakie pytanie powinien zadać, żeby z całą pewnością wybrać właściwą drogę do restauracji?

Rozwiązanie : Skonstruujmy pytanie w taki sposób, by niezależnie od tego, czy odpowiadający jest prawdomówny, czy nie, odpowiedź twierdząca oznaczała, że turysta ma udać się w lewo, a odpowiedź przecząca, że ma udać się w prawo. Niech p oznacza typ tubylca:

p = 1 - prawdomówny, p = 0 - kłamca,

a q określa wybór drogi do restauracji:

q = 1 - do restauracji trzeba się udać w lewo, q = 0 - do restauracji trzeba się udać w prawo.

Wynika stąd, że pytanie x, które mamy zadać, ma następującą matrycę logiczną

Jeśli na nasze pytanie odpowiadał prawdomówny, to postępujemy tak jak na to wskazuje zmienna q. Jeśli na nasze pytanie odpowiadał kłamca, to postąpimy odwrotnie niż na to wskazuje zmienna q. Z przedstawionej matrycy wynika, że pytanie powinno mieć postać (p ∧ q) ∨ ( ¬ p ∧ ¬ q). Brzmi ono zatem: Czy prawdziwe jest zdanie "Jesteś prawdomówny wtedy i tylko wtedy, gdy do restauracji trzeba iść w lewo"?

Istnieje bardzo ścisły związek reguł wnioskowania i tautologii rachunku zdań. Reguły prowadzą zawsze od tautologii do tautologii. Co więcej, każda tautologia w postaci implikacji może być przekształcona w poprawną regułę wnioskowania i odwrotnie, każda poprawna reguła wnioskowania odpowiada pewnej tautologii. Związki te zanotowaliśmy w postaci lematów 7.6.2 i 7.6.3.

Lemat 7.6.3

Niech α ₁,..., α _n, β będą formułami rachunku zdań. Formuła ( α _{1 ∧} ... ∧ α _n) → β jest tautologią, wtedy i tylko wtedy, gdy

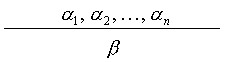
jest regułą dowodzenia.

Reguły dowodzenia pozwalają wydedukować nowe tautologie z innych, już znanych. Powstaje pytanie, czy można zbudować system złożony z niewielkiej liczby najprostszych tautologii i pewnych reguł, które pozwolą wyprowadzić wszystkie inne tautologie rachunku zdań. Takie podejście nazywa się aksjomatycznym, a odpowiedź na to pytanie jest twierdząca.

Jako tautologie bazowe, mówimy o nich aksjomaty rachunku zdań, można przyjąć cztery prawa logiki (schematy) przedstawione na rysunku Rys. 7.6.1, a jako jedyną regułę dowodzenia - regułę modus ponens.

Rys. 7.6.1 Aksjomaty rachunku zdań

Poniżej podamy dokładną definicję procesu dowodzenia, tzn. pojęcia dowodu formalnego w Rachunku Zdań.

Przykład 7.6.3

Następujący ciąg formuł jest dowodem formalnym formuły (α → α).

1. ( α → (( α → α) → α))    tautologia postaci (a → (b → a))    (prawo symplifikacji)

2. ( α → ( α → α))    prawo symplifikacji

3. ( ( α → (( α → α) → α)) → (( α → ( α → α)) → ( α → α)))    prawo Fregego
   ((a → (b → c)) → ((a → b) → (a → c)))

4. (( α → ( α → α)) → ( α → α))    z (a) i (c) przez zastosowanie modus ponens

5. ( α → α)    z (d) i (b) przez zastosowanie modus ponens

Dowód formalny wygodnie jest zapisać w postaci drzewa binarnego (por. Rys.7.6.2), w którym etykietą korzenia jest formuła, której dowodzimy, etykietami liści są aksjomaty użyte w dowodzie, a wszystkie wierzchołki wewnętrzne drzewa mają etykiety zgodnie z zasadą: jeśli x jest wierzchołkiem, którego synami są wierzchołki o etykietach γ i ( γ → β), to etykietą wierzchołka x jest β.

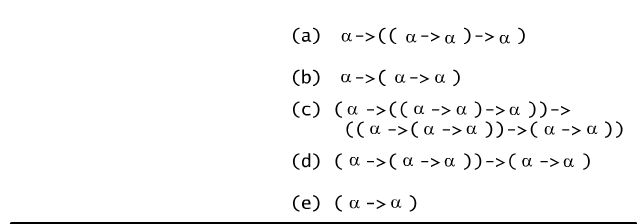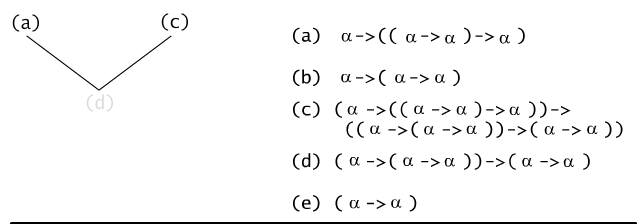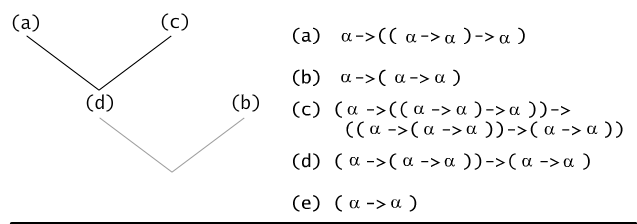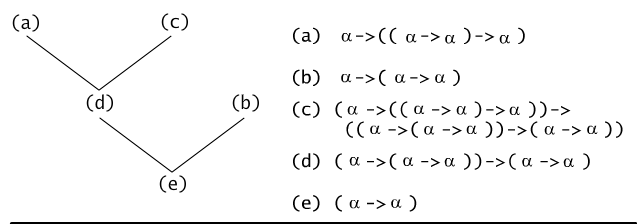
Rys. 7.6.2 Drzewo dowodu formalnego formuły ( α → α).

Na zakończenie zanotujmy jeszcze, że system aksjomatyczny rachunku zdań ma własność pełności, tzn. wszystko co w nim udowodnimy jest zawsze prawdziwe i każde zdanie, które jest prawdziwe można udowodnić w tym systemie. W ten sposób zyskaliśmy jeszcze jedną metodę dowodzenia tautologii - metodę formalną. Nie należy jednak sądzić, że jest to metoda mniej kosztowna niż metoda zerojedynkowa. Znalezienie dowodu formalnego wymaga czasami wiele pomysłowości, a zatrudnienie do tego celu komputera będzie pochłaniało tyle samo czasu co metoda zerojedynkowa.

Uwaga. Na ogół nie przeprowadza się dowodów formalnych. Ważny jest jednak fakt, że dowód formalny można, o ile zajdzie taka konieczność, przeprowadzić i drobiazgowo sprawdzić wszystkie jego etapy.