Czasami będziemy używali oznaczenia α(a/x) dla zaznaczenia, że mamy do czynienia ze zdaniem, które powstało przez wstawienie konkretnej wartości a na miejsce zmiennej x.

Ogół tych wartości, dla których funkcja zdaniowa α(x) jest spełniona oznaczamy przez {x ∈ X: α(x)}. Dokładniej należałoby napisać

ale będziemy używać krótszego zapisu, o ile nie będzie to prowadziło do nieporozumień.

Każda funkcja zdaniowa wyznacza więc pewien podzbiór (pewną własność) przestrzeni, w której została określona, a mianowicie zbiór tych argumentów, dla których jest spełniona.

Dowód.

Dla przykładu udowodnimy jedynie pierwszy z podanych wzorów. Analogiczne dowody dla pozostałych równości pozostawiamy Czytelnikowi.

Niech a ∈ {x ∈ X: α(x)} ∪ {x ∈ X: β(x)}. Wtedy, na mocy definicji sumy teoriomnogościowej zbiorów, element a należy do co najmniej jednego ze zbiorów {x ∈X: α(x)}, {x ∈X: β(x)}. Oznacza to, że a spełnia funkcję zdaniową α(x) lub a spełnia funkcję zdaniową β(x), czyli alternatywa α(a/x) ∨β(a/x) jest zdaniem prawdziwym. Stąd a ∈ {x ∈ X: α(x) ∨ β(x)}.

Odwrotnie, jeśli a ∈ {x ∈ X: α(x) ∨ β(x)}, to α(a/x) ∨ β(a/x) jest zdaniem prawdziwym. Na mocy praw dwuelementowej algebry Boole'a (por. 7.2), chociaż jedno ze zdań α(a/x), β(a/x) jest zdaniem prawdziwym. Wynika stąd, że a należy chociaż do jednego ze zbiorów {x ∈ X: α(x)}, {x ∈ X: β(x)}, czyli a ∈ {x ∈ X: α(x)} ∪ {x ∈ X: β(x)}. ♦

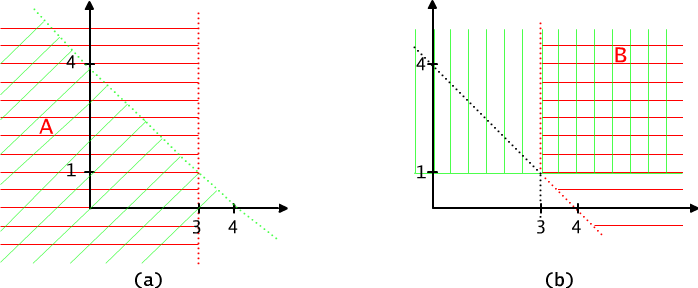
Rys. 8.2.1 Zbiór punktów płaszczyzny spełniających (a) funkcję zdaniową ((x-3 < 0) ∨(x+y< 4)), (b) funkcję zdaniową ¬ ((x-3 < 0) ∨ (x+y< 4)) ∧ (1 ≤ y).

Przykład 8.2.1

1. Niech ¬ ((x-3 < 0) ∨(x+y< 4)) ∧ (1 ≤ y) będzie funkcją zdaniową dwóch zmiennych x, y, określoną w zbiorze liczb rzeczywistych R. Wyliczmy najpierw zbiór tych par liczb (x,y), które spełniają funkcję zdaniową ((x-3 < 0) ∨ (x+y < 4)). Niech A = {(x,y) ∈ R²: ((x-3 < 0) ∨(x+y < 4))} = {(x,y) ∈ R²: x<3} ∪ {(x,y) ∈ R²: x+y<4}, por. Rys. 8.2.1(a). Następnie znajdziemy wszystkie pary spełniające naszą funkcję zdaniową wykonując odpowiadające operacje na zbiorach, tzn. wyliczając -A ∩ {(x,y) ∈ R²: 1 ≤ y}. Wynik, tzn. wszystkie pary postaci (x,y), dla których 3 ≤ x i 1 ≤ y, zaznaczono na rysunku 8.2.1(b).
2. Funkcja zdaniowa (A ∪ B ⊆ C → (A ⊆ C ∧ B ⊆ C)) trzech zmiennych A, B, C, przebiegających podzbiory pewnego ustalonego uniwersum U, jest spełniona dla wszystkich elementów produktu P(U)³, tzn. jakiekolwiek konkretne zbiory wstawimy jako wartości zmiennych A, B, C, to otrzymane zdanie będzie prawdziwe, por. punkt 1.3. Rzeczywiście, ponieważ warunek A ∪ B ⊆ C jest równoważny (A ∪ B) ∪ C = C, zatem A ∪ C = A ∪ (A ∪ B ∪ C) = A ∪ B ∪ C = C oraz B ∪ C = B ∪ (A ∪ B ∪ C) = A ∪ B ∪ C = C. Stąd A ⊆ C oraz B ⊆ C.

Pytanie 8.2.1 Dla jakich wartości x spełniona jest funkcja zdaniowa ((x ≤ 1 ∨ x >1) → x² =1) określona w zbiorze liczb rzeczywistych?

« poprzedni punkt

następny punkt »