Ciąg nieskończony jest to, jak wiadomo (por. wykład IV) funkcja całkowita określona na zbiorze liczb naturalnych N. Jednym z wygodnych sposobów określania wyrazów ciągu jest definicja indukcyjna. Ten sposób definiowania polega na określeniu pierwszego wyrazu ciągu (lub kilku pierwszych wyrazów) np. a0, i podaniu metody konstrukcji wyrazu (n+1)-go w zależności od wyrazu n-tego lub innych wyrazów już zdefiniowanych. Przyjrzyjmy się przykładom.

Przykład 9.4.1

(1) Przyjmijmy następującą definicję ciągu (a_i) _{i ∈ N} :

a₀ = 1, a_n+1 = a_n + 2 dla wszystkich n ≥ 0.

Łatwo wyliczyć, że a₁ = a₀ + 2 = 1+2 = 3, a₂ = a₁ +2 = 5 itd. Przyglądając się bliżej tym definicjom zauważymy, że a₁ = a₀ + 2 = 1+ 1 ⋅2 , a₂ = 1 +2 ⋅2 = 5, a₃ = 1 +2 ⋅2 +2 = 1 +3 ⋅2.

Domyślamy się, że a_k = 1+ k ⋅2 dla wszystkich k>0.

Stosując zasadę indukcji matematycznej możemy pokazać, że a_k = 1+ 2k dla wszystkich k.

Rzeczywiście, dla k=0 otrzymujemy a₀ = 1. Natomiast krok indukcyjny wynika z indukcyjnej definicji ciągu, założenia indukcyjnego dla k i prostego przekształcenia wzoru: a_k+1 = a_k + 2 = (1+ 2k) + 2 = 1+ 2(k+1).

(2) Przyjmijmy definicję ciągu b = (b_i) _{i ∈ N} :

b₀ = 1, b₁ = 1, b_n+1 = b_n ⋅ (n+1) dla wszystkich n ≥ 0.

Wyliczmy kilka pierwszych wyrazów tego ciągu:

b₁ = b₀ ⋅ 1 = 1, b₂ = b₁ ⋅2 = 2, b₃ = b₂ ⋅ 3 = 6, b₄ = b₃ ⋅4 = 24 itd.

Łatwo udowodnimy, że b_n = 1 ⋅2 ⋅3 ⋅... ⋅n = n!

Zadanie 9.4.1 Stosując zasadę indukcji matematycznej udowodnić, że n-ty wyraz ciągu b z przykładu 9.4.1 ma postać b_n = n!

Rozwiązanie: Dla n=0 i dla n=1 twierdzenie jest prawdziwe: b₀=1 i b₁=1!. Załóżmy, że b_i=i! dla pewnego i>0. Na mocy definicji elementów ciągu mamy b_i+1= b_i ⋅ (i+1). Po wykorzystaniu założenia indukcyjnego mamy b_i+1 = i! ⋅ (i+1)= (i+1)!. Na mocy zasady indukcji twierdzenie jest prawdziwe dla wszystkich liczb naturalnych >0. ♦

Przykład 9.4.2

Niech będzie ciąg określony z pomocą następującej definicji indukcyjnej

f₀ = 0, f₁ = 1, f_n+2 = f_n + f_n+1

Ciąg ten nazywa się ciągiem Fibonacciego.

Oczywiście, z definicji łatwo można wyliczyć jaka jest wartość kolejnych wyrazów tego ciągu. Wymaga to jednak pewnej systematyczności i cierpliwości. Na przykład dla f₇ mamy f₇ = f₅ + f₆ = f₅ + f₄ + f₅ = 2(f₃ + f₄ ) + f₄ = 3(f₂ + f₃) + 2 f₃ = 5(f₂ + f₁) + 3f₂ = 8(f₀ + f₁ )+ 5 f₁ = 13.

Za pomocą indukcji można udowodnić, że dla wszystkich liczb naturalnych n, zachodzi wzór

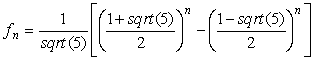
Baza indukcji. Wartość po prawej stronie wzoru wynosi 0 dla n=0, a z definicji indukcyjnej mamy też f₀ = 0.

Założenie indukcyjne. Zakładamy, że wzór jest słuszny dla wszystkich liczb naturalnych mniejszych od k+2.

Teza. Udowodnimy, że wzór jest prawdziwy dla k+2.

Dowód tezy indukcyjnej. Dla uproszczenia dowodu przyjmijmy oznaczenia

Założenie indukcyjne przyjmuje teraz postać f_i = c(aⁱ -bⁱ) dla i <k+2. Wykorzystując to założenie dla k i dla k+1, oraz indukcyjną definicję ciągu otrzymujemy:

f_k+2 = f_k + f_k+1 = c(a^k -b^k) + c(a^k+1 -b^k+1) = c [a^k (1 + a) - b^k(1 + b)]

Ponieważ 1+a = a², a 1+b = b², zatem f_k+2 = c(a^k+2 -b^k+2).

Na mocy zasady indukcji matematycznej każdy wyraz ciągu Fibonacciego wyraża się podanym wyżej wzorem.

Niech będzie dany ciąg a₀, a₁, a₂,..., którego wyrazami są liczby. Sumę n pierwszych elementów tego ciągu oznaczamy przez

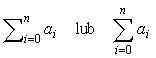
i czytamy "suma a_i dla wszystkich i od 0 do n.". Gdy chcemy posumować nie wszystkie wyrazy ciągu, a tylko zaznaczony fragment, lub tylko te wyrazy, dla których spełniony jest pewien specjalny warunek w, piszemy

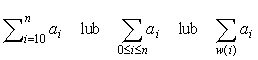
Taki zapis jest jednoznaczny i często wygodniejszy przy przekształceniach niż zapis a₀ + ... +a_n , w którym trzeba się domyślić co oznaczają kropki. Czy każdy domyśla się jaka jest kolejna liczba w ciągu 0,1,1,2,3,...?

Oczywiście wybór literki wskazującej, jakie elementy sumujemy, nie ma znaczenia. Czyli

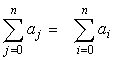
W podobny sposób oznacza się iloczyny. Iloczyn (n+1) wyrazów ciągu (a_i)_{i ∈ N} możemy zapisać w postaci a₀ ⋅ ... ⋅a_n lub

Pytanie 9.4.1: Jaka jest wartość wyrażenia?

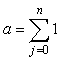
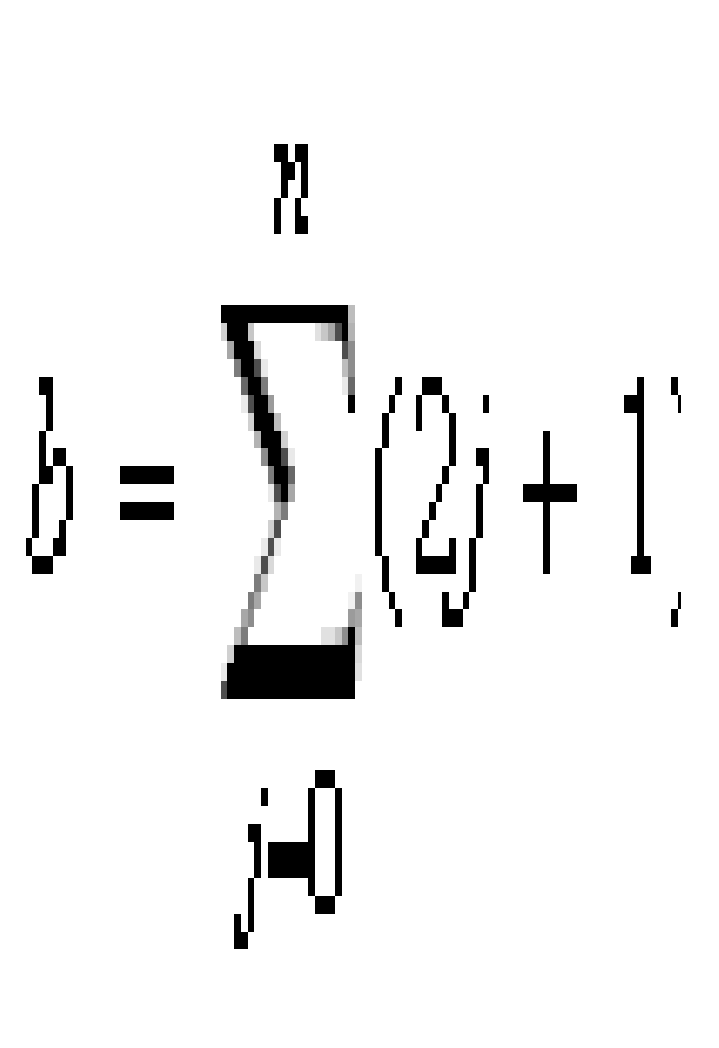
Przykład 9.4.3

Rozważmy następujący ciąg liczb: a₁= 1, a_n = a_n-1 + 1 i utwórzmy nowy ciąg b, którego n-tym elementem jest suma pierwszych n wyrazów ciągu (a_i) _{i ∈N}, tzn. b₁ = a₁, b_n = a₁ +...+a_n. Elementy tego ciągu nazywa się liczbami trójkątnymi (Jeśli chcesz wiedzieć dlaczego, zobacz rysunek 4.1.3) Najpierw zauważymy, że dla dowolnego i, a_i = i, co można pokazać stosując zasadę indukcji. Kolejne wyrazy ciągu b przyjmują wartości: b₁ = 1, b₂ =3, b₃ = 6, b₄ = 10, b₅ = 15. Udowodnimy, że

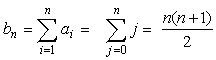
Dowód.

Mamy (1+1) ⋅1/2 =1, czyli wzór jest prawdziwy dla n=1 (baza indukcji).

Załóżmy, że wzór jest słuszny dla n=k, czyli

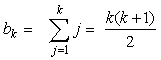
Korzystając z tego założenia i definicji ciągu b otrzymujemy:

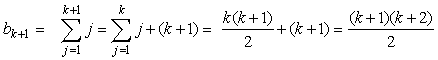
Zatem, na mocy zasady indukcji, wszystkie wyrazy ciągu są postaci b_n = n(n+1)/2.

Pytanie 9.4.2: Ile wynosi iloczyn pierwszych n wyrazów ciągu a₀ = 2, a_i+1 = 4a_i dla i>0?

Zadanie 9.4.2 Udowodnić przez indukcję, że suma n pierwszych wyrazów ciągu a zdefiniowanego następująco a₀= 1, a₁=2, a_n = 2a_n-1 dla n>1, wynosi 2ⁿ -1.

Podpowiedź: Najpierw pokazać przez indukcję, że n-ty wyraz ciągu wyraża się wzorem a_n =2ⁿ , a następnie, również stosując rozumowanie indukcyjne ze względu na liczbę składników sumy, udowodnić, że suma 1+2 + ...+ 2^n-1 wynosi 2ⁿ -1.