| « poprzedni punkt | następny punkt » |
W poprzednim punkcie wykładu skupiliśmy się na definicjach indukcyjnych ciągów nieskończonych i rozwikływaniu tych definicji. Teraz zajmiemy się definiowaniem innego typu funkcji i to niekoniecznie jednoargumentowych. Metoda jaką tu zastosujemy nazywa się definiowaniem przez rekursję. Na czym to polega? Proste: aby zdefiniować wartość operacji dla pewnych argumentów wykorzystujemy wartości tej samej operacji dla innych prostszych argumentów. Inaczej mówiąc: rozwiązanie dużego problemu sprowadzamy do rozwiązań konkretnych mniejszych problemów.
Przykład 9.5.1
(1) Dodawanie w zbiorze liczb naturalnych z zerem i następnikiem (tak jak to definiują aksjomaty Peano), można zdefiniować następująco:
n + 0 = n, dla dowolnego n ∈ N,
n + suc(m) = suc(n + m) , dla dowolnych n, m ∈ N.
Korzystając z tej definicji i aksjomatów Peano liczb naturalnych, można udowodnić wszystkie znane własności operacji sumy, np. przemienność i łączność dodawania.
(2) Operację mnożenia w zbiorze liczb naturalnych możemy zdefiniować w podobny sposób:
n ⋅ 0 = 0, dla dowolnego n ∈ N
n ⋅ suc(m) = (n ⋅ m) + n, dla dowolnych n, m ∈ N.
Korzystając z tej definicji i aksjomatów Peano, można udowodnić, że mnożenie jest dobrze określoną operacją dla wszystkich par liczb naturalnych. Można też pokazać wszystkie inne własności iloczynu.
Dla przykładu podamy dowód indukcyjny prawa rozdzielności.
Lemat 9.5.1
Dla dowolnych liczb naturalnych m, n, k,
(m + n) ⋅ k = m ⋅ k + n ⋅ k.
Dowód.
Niech m i n mają dowolnie ustalone wartości. Oznaczmy powyższy wzór przez W(k).
Jeśli k=0, to (m+ n) ⋅ k =(m+ n) ⋅ 0 =0 na mocy definicji operacji mnożenia, oraz m ⋅ k + n ⋅ k = m ⋅ 0 + n ⋅ 0 = 0+0 na podstawie definicji mnożenia. Teraz, z pierwszej równości definiującej dodawanie, otrzymujemy 0+0 =0, czyli W(0).
Załóżmy, że wzór jest prawdziwy dla pewnego k, tzn. zakładamy prawdziwość W(k). Na mocy definicji operacji dodawania i mnożenia oraz praw przemienności i łączności dodawania mamy
(m+ n) ⋅ suc(k) =(m+ n) ⋅ k + (n +m) = (m ⋅ k + m) + (n ⋅ k+n) = m ⋅suc(k) + n ⋅suc(k).
Zatem, na mocy zasady indukcji matematycznej, dla dowolnego naturalnego k, W(k). Wynika stąd, że omawiane prawo rozdzielności jest prawdziwe dla wszystkich wartości m, n, k.
Zadanie 9.5.1 Zdefiniuj rekurencyjnie operację podnoszenia do potęgi w zbiorze liczb naturalnych.
Odpowiedź: a0 =1, an+1 = an a.
Definicje rekurencyjne są chętnie wykorzystywane w programowaniu. Bardzo często definicja rekurencyjna daje o wiele czytelniejszy kod niż definicja rozwikłana.
Przykład 9.5.2 Algorytm Euklidesa
Oznaczany przez nwd(n,m) największy wspólny dzielnik liczb n i m. Matematyczna definicja tej operacji dwuargumentowej może być zapisana następująco:
nwd(n,m) = k ≡ (k|n ∧ k|m) ∧ ( ∀ x) ((x|n ∧ x|m ) → x|k)
Łatwo wyliczyć wartość nwd dla konkretnych niewielkich liczb, np. nwd(4,6)= 2, nwd(12,6) = 6, nwd(36,27)= 9 itd. rozkładając liczby na czynniki pierwsze. Nie jest to jednak sposób prosty zwłaszcza wtedy, gdy liczby są duże. Na szczęście w sukurs przychodzi nam matematyka. Wiadomo, że zachodzą następujące równości
nwd(x,y) = nwd(y,x), nwd(x,0) = x
nwd(x,y) = nwd(y, x mod y), gdy y ≠ 0 oraz x ≥y
nwd(x,y) = nwd(x, y - x), gdy y>x
nwd(x,y) = nwd(x - y, y), gdy x>y.
Te własności największego wspólnego dzielnika sugerują proste algorytmy (nwd1 lub nwd2) obliczania wartości nwd dla dowolnych x, y ∈ N:
nwd1(x,y) {
if x = y then return x
else if y>x then return nwd1(x, y - x) else return
nwd1(x - y, y) fi
fi
}
nwd2(x,y) {
if y=0 then return x else
return nwd2 (y, x mod y) fi
}
Algorytmy nwd1 i nwd2 są procedurami rekurencyjnymi. Aby obliczyć wartości nwd dla x i y musimy najpierw wyliczyć, przy pomocy tej samej procedury, wartości nwd dla innych argumentów, tzn. wywołujemy rekurencyjnie w treści procedury tę samą procedurę. Przykładowe łańcuchy kolejnych rekurencyjnych wywołań procedury nwd1 są przedstawione na rysunku 9.5.1.
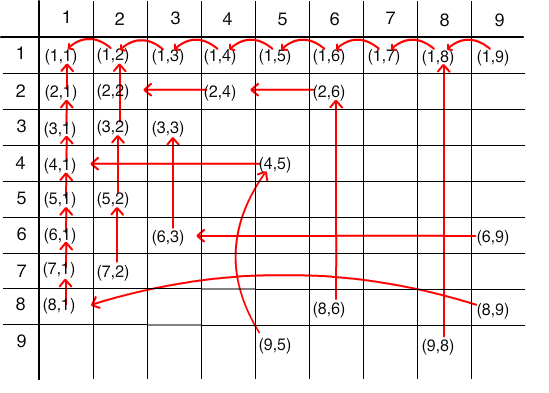
Rys. 9.5.1 Łańcuchy wywołań rekurencyjnych procedury nwd1.
Przykład 9.5.3 Chodzenie po grafie
Niech będzie dane drzewo binarne G o korzeniu w R (por. Rys. 9.5.2) i niech dla dowolnego wierzchołka x tego drzewa będą określone funkcje lewy(x) i prawy(x), których wartością jest wierzchołek będący lewym następnikiem x lub odpowiednio prawym następnikiem x, lub wartość specjalna none, w przypadku, gdy wierzchołek x nie ma odpowiedniego następnika. Przyjmujemy, że R ≠ none. Następująca procedura GO jest rekurencyjną definicją sposobu odwiedzania wierzchołków drzewa G.
GO (G,x){
if x ≠ none then
odwiedź(x);
GO(G, lewy(x));
GO (G, prawy(x));
fi;
}
Jeśli wywołamy tę procedurę dla grafu przedstawionego na rysunku 9.5.2 i z wartością x=R, to kolejność odwiedzania będzie następująca : RAopulbGLOTYĘIMK!
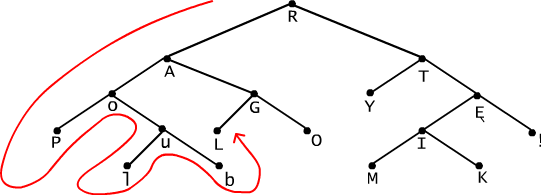
Rys. 9.5.2 Odwiedzanie wierzchołków drzewa. Kolejność wyznaczona przez procedurę GO: RAopulbGLOTYĘIMK!
Pytanie 9.5.1 Jaka będzie kolejność odwiedzania wierzchołków grafu przedstawionego na rysunku 9.5.2, jeśli instrukcję odwiedź(x) umieścimy między rekurencyjnymi wywołaniami procedury GO ?
Zadanie 9.5.2 Sprawdź działanie procedury GO na innych przykładach.
Uwaga na kłopoty
Przypuśćmy, że wprowadzimy definicję rekurencyjną pewnej operacji w zbiorze liczb naturalnych następująco:
coś(x,0) = 0,
coś(x, y+1) = coś(x,y+1)+1.
Takiej definicji nie możemy jednak zaakceptować. Nie umiemy wyliczyć wartości coś(x,y+1), bo w podanym wzorze po obu stronach równości występuje to samo wyrażenie. Gdybyśmy natomiast przypuścili, że coś(x,y+1) ma wartość np. a, to doprowadzi nas to do sprzeczności, gdyż wtedy 0=1.
Aby uniknąć sprzeczności definicja rekurencyjna powinna mieć postać
h(x,0)= f(x)
h(x,y+1) = g(x,y,h(x,y))
dla pewnych danych funkcji f(x) i g(x,y,z).
Warto o tym pamiętać, szczególnie wtedy, gdy w programie definiujemy funkcje w sposób bardzo zawikłany, odwołując się wielokrotnie do definiowanej funkcji i do innych funkcji.
Zadanie 9.5.3 Podaj rekurencyjną definicję operacji min znajdowania minimum w danym ciągu liczbowym a[0], a[1],..., a[n].
Odpowiedź:
min(a,0) = a[0], min(a,n) = a[n], gdy a[n]<min(a, n-1), min(a,n) = min(a,n-1), gdy a[n]> min(a,n-1).
| « poprzedni punkt | następny punkt » |