Podstawowe pytanie, jakie stawia sobie kombinatoryka jest bardzo proste: mając pewną liczbę obiektów i pudełek, na ile różnych sposobów można umieścić te obiekty w pudełkach?

Rozważmy na początek 10 różnych klocków i 4 pudełka, i zadanie, które rozwiązywaliśmy jako dzieci: ułożyć klocki w pudełkach. Ile jest możliwych realizacji tego zadania? Jeśli klocki ponumerujemy liczbami od 0 do 9, to klocek o numerze 0 możemy włożyć do pierwszego, drugiego, trzeciego lub czwartego pudełka. Cztery możliwości. Podobnie, drugi klocek możemy włożyć do jednego z czterech pudełek. Łatwo zauważyć, że tak samo jest dla każdego następnego klocka. Zatem różnych sposobów rozmieszczenia klocków w czterech pudełkach jest 4 ¹⁰. Strasznie dużo!

Rozważmy teraz nieco bardziej "dorosły" (abstrakcyjny) przykład. Dane są dwa zbiory X i Y takie, że |X| = n i |Y| = m.

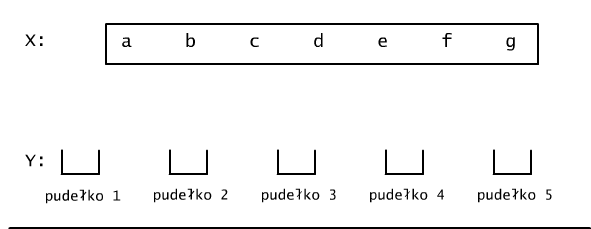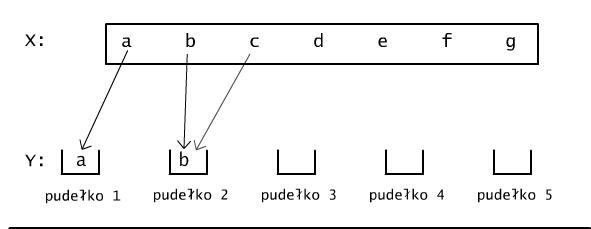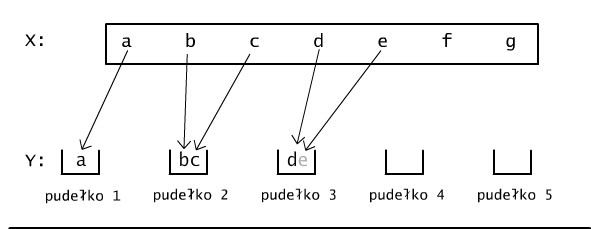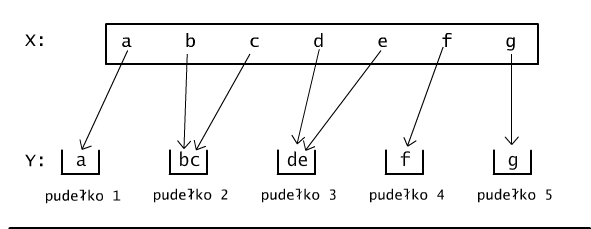
Rys. 11.1.1 Elementy zbioru X rozmieszczamy w pudełekach ponumerowanych elementami zbioru Y.

Ile można zdefiniować różnych funkcji całkowitych, określonych w zbiorze X i o wartościach w zbiorze Y?

Elementy zbioru Y możemy potraktować jak pudełka, do których wrzucać będziemy elementy zbioru X, por. Rys.11.1.1. Oznacza to, że w tworzonej funkcji f, wszystkie elementy x, które trafiły do pudełka y będą miały wartość określoną jako f(x) = y. Ponieważ każdy z elementów zbioru X może trafić do dowolnego z m pudełek, lub inaczej mówiąc, każdej wartości argumentu x możemy przyporządkować dowolną z wartości wziętą ze zbioru Y, zatem wszystkich sposobów zdefiniowania funkcji z X w Y jest

m × m × ... × m

n razy

czyli mⁿ. Udowodniliśmy tym samym twierdzenie

Zauważmy, że natura obiektów, z których składają się zbiory X i Y nie była w naszych rozważaniach istotna. Możemy zatem przyjąć, że zarówno zbiór X jak zbiór Y są zbiorami liczb naturalnych, X = {1,2,...,n} i Y = {1,2,...,m}(Gdyby zresztą tak nie było, to, ponieważ oba zbiory są skończone, ich elementy możemy po prostu ponumerować liczbami naturalnymi.). Każdą funkcję całkowitą ze zbioru X w zbiór Y możemy teraz scharakteryzować podając ciąg jej wartości dla kolejnych argumentów

f(1), f(2),..., f(n).

Wartością na każdej pozycji może być jedna z liczb 1,...m, czyli różnych takich ciągów jest dokładnie m * m * ... (n krotnie) * m, czyli m ⁿ.

Wniosek

Liczba różnych ciągów n elementowych o wyrazach ze zbioru m-elementowego wynosi m ⁿ.

Rozważmy teraz kilka przykładów zastosowań twierdzenia 11.1.1.

Przykład 11.1.1

Na ile sposobów można wylosować pięć kart z talii 52 kart, jeśli po każdym losowaniu odkładamy wylosowaną kartę do talii?

Rozwiązanie

Aby ułatwić odpowiedź, przepiszmy pytanie w nieco innych terminach. Każde 5 wylosowanych kart tworzy pięcioelementowy ciąg. Pytamy więc ile można utworzyć różnych pięcioelementowych ciągów, których wyrazy należą do zbioru o 52 elementach. Albo jeszcze inaczej: wylosowany zestaw kart możemy traktować jako funkcję, która mówi jaką kartę wylosowaliśmy jako pierwszą, jaką jako drugą, itd. Pytamy zatem, ile jest funkcji określonych na zbiorze 5-cio elementowym o wartościach w zbiorze 52 elementowym. Na mocy twierdzenia 11.1, odpowiedź brzmi 52 ⁵.

Przykład 11.1.2

Dany jest graf o n wierzchołkach ponumerowanych od 1 do n. Dysponujemy k kolorami. Na ile sposobów możemy pokolorować wierzchołki tego grafu?

Rozwiązanie

Pokolorowanie, to inaczej przypisanie wierzchołkowi koloru. W terminach funkcji pytanie brzmi więc: ile jest różnych funkcji ze zbioru wierzchołków w zbiór kolorów? Możemy też sformułować je w terminologii rozmieszczeń: na ile sposobów można rozmieścić wierzchołki grafu w k kolorowych pudełkach. Na mocy twierdzenia 11.1.1,. odpowiedź brzmi k ⁿ.

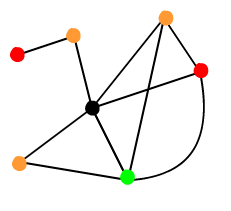
Rys. 11.1.2 Różne pokolorowania grafu.

Pytanie 11.1.1: Ile jest różnych pokolorowań grafu na rysunku 11.2 czteroma kolorami, takich że dwa wierzchołki sąsiednie mają różne kolory?

Przykład 11.1.3

Ile różnych liczb całkowitych można zapisać w n-bitowym rejestrze.

Rozwiązanie

Każdej liczbie całkowitej odpowiadać będzie ciąg zerojedynkowy o długości n. Zatem pytanie powyższe brzmi, ile jest różnych ciągów n-elementowych, których wyrazami są zero i jeden? Albo inaczej, ile jest różnych funkcji przyjmujących tylko dwie wartości, a określonych w zbiorze n-elementowym? Oczywiście jest ich 2 ⁿ, znów na mocy twierdzenia 11.1.1.

Przykład 11.1.4

Oszacować liczbę słów w słowniku pewnego języka, jeśli jego alfabet składa się z 24 liter, a słowa składają się z co najwyżej 20 liter.

Rozwiązanie

Każde słowo, to skończony ciąg liter. Ciągów o długości k jest w tym języku co najwyżej tyle ile jest funkcji ze zbioru k elementowego w zbiór 24 elementowy, czyli 24^k. Ponieważ k może się zmieniać od 1 do 20, zatem wszystkich słów może być co najwyżej 24¹ + 24² +...+ 24²⁰ = (24 ²¹ -1)/23.

Pytanie 11.1.1: Najczęściej występujące na flagach państwowych kolory to kolory podstawowe: czerwony, niebieski, zielony, żółty, biały i czarny. Ile co najwyżej flag można utworzyć z tych kolorów, jeśli wszystkie flagi składają się z trzech poziomych pasów? Uwaga, kolory mogą się powtarzać(np. wszystkie trzy pasy mogą mieć ten sam kolor.

« poprzedni punkt

następny punkt »