| « poprzedni punkt | następny punkt » |
W poprzednich paragrafach tego wykładu zwracaliśmy uwagę na kolejność w jakiej występowały wybierane elementy. Spróbujmy teraz o tym zapomnieć.
Rozważmy jeszcze raz przykład z talią kart. Załóżmy, że w pewnej grze każdy gracz otrzymuje pięć kart i graczowi jest obojętne w jakiej kolejności je otrzyma, gdyż np. gra rozpoczyna się dopiero wtedy, gdy otrzyma wszystkie 5 kart. Jeśli tak, to 5-elementowe zestawy
D, K, 10, 9, W
K, 10, 9, W, D
są takie same.
Oznacza to, że zamiast ciągów kart, rozważamy zbiory kart. Ile zatem różnych 5-elementowych zbiorów kart można wylosować z 52-elementowej talii?
Ponieważ każdy z 5! ciągów (wszystkie permutacje tego samego zestawu) jest teraz rozumiany jako ten sam zbiór, to liczba zbiorów jest 5! razy mniejsza niż liczba 5-elementowych ciągów kart. Czyli wynosi
Definicja 11.5.1
Liczbę k-elementowych podzbiorów zbioru n-elementowego oznaczamy
przez 
i nazywamy symbolem
dwumianowym Newtona.
k-elementowe podzbiory zbioru n-elementowego nazywamy k-elementowymi
kombinacjami.
Jako wniosek z twierdzeń 11.4.1 i 11.2.1 otrzymujemy następujące twierdzenie 11.5.1.
Twierdzenie 11.5.1
Liczba k-elementowych kombinacji w dowolnym zbiorze n-elementowym wynosi
Zadanie 11.5.1 Udowodnić korzystając z twierdzenia 11.5.1, że
dla dowolnych n, k, jeśli n ≥ k, to 
.
Korzystając z interpretacji symbolu , łatwo uzasadnić, że
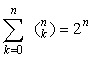
Rzeczywiście, podzbiory zbioru n-elementowego to: zbiór pusty, wszystkie podzbiory jednoelementowe, wszystkie podzbiory 2-elementowe, itd. Lewa strona rozważanej równości zlicza wszystkie podzbiory zbioru n-elementowego. Wiemy skądinąd, że wszystkich podzbiorów w zbiorze n elementowym jest 2 n (por. wykład 1) i stąd rozważana równość.
Pytanie 11.5.1: Powiemy, że dwa numery rejestracyjne samochodów są podobne, jeśli zbiory znaków z których zostały zbudowane są identyczne. Ile niepodobnych numerów rejestracyjnych samochodów można utworzyć w Warszawie, jeśli każdy numer składa się z trzech różnych liter, z których pierwsza to W, a pozostałe dwie należą do zbioru {A,B,C,Z}, i z pięciu pozycji, na których znajdują się cyfry?
| « poprzedni punkt | następny punkt » |