Użyjemy jeszcze raz rozumowania związanego z interpretacją symbolu, aby wyprowadzić pewien pożyteczny wzór. Niech X będzie n-elementowym zbiorem i a pewnym jego wyróżnionym elementem, a ∈X. Podzielimy wszystkie k-elementowe podzbiory zbioru X na dwie kategorie:

1. wszystkie k-elementowe podzbiory X, do których a nie należy,
2. wszystkie k-elementowe podzbiory X, do których a należy.

Oczywiście, tych pierwszych jest , bo wybieramy k-elementowe podzbiory zbioru X-{a}. Zbiorów drugiej kategorii jest , bo składają się one z elementu a i dowolnego (k-1)-elementowego podzbioru zbioru X-{a}. Ponieważ do każdego podzbioru zbioru X albo a należy albo a nie należy, zatem suma tych zbiorów, to wszystkie podzbiory k-elementowe.

Udowodniliśmy tym samym następujący wzór

Okazuje się, że wzór ten jest niezwykle przydatny, gdy chcemy wyliczyć wartość symbolu Newtona dla konkretnych n i k. Utworzymy w tym celu tablicę w postaci trójkąta prostokątnego (por.Rys.11.6.1(a)). Jeden bok i przeciwprostokątna tego trójkąta są wypełnione jedynkami, natomiast kolejne pozycje n-tego wiersza są wypełnione liczbami wyliczonymi z właśnie udowodnionego wzoru (*): dodajemy dwie pozycje z poprzedniego wiersza z sąsiedniej (tzn. (k-1)-szej) i tej samej (tzn. k-tej) kolumny. Proste.

Opisany trójkąt nosi nazwę trójkąta Pascala i zwykle jest przedstawiany jak na rysunku Rys.11.6.1(b). Czytelnik zechce samodzielnie napisać i zaimplementować algorytm wyliczania wartości symbolu Newtona dla dowolnych n i k, zgodnie z zasugerowanym algorytmem.

Pytanie 11.6.1: Dlaczego, w tym przypadku, nie jest rozsądnym rozwiązaniem napisanie algorytmu rekurencyjnego?

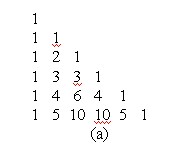
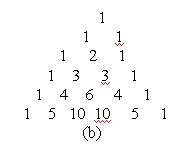
Rys. 11.6.1 Trójkąt Pascala

Zadanie-Zabawa (Trójkąt Sierpińskiego) Napisz program, który drukuje trójkąt Pascala w postaci 11.6.1(b), ale tak, że wszystkie liczby nieparzyste zostały zastąpione kropkami, a liczby parzyste odpowiednimi odstępami (puste miejsca). Porównaj uzyskany obraz z wynikiem następującego procesu: Trójkąt równoboczny podziel na cztery jednakowe trójkąty równoboczne i wytnij środkowy. Następnie zrób to samo z każdym z pozostałych trzech trójkątów. Otrzymasz 9 trójkątów równobocznych i znów z każdego z nich wytnij środkowy trójkąt równoboczny. itd. A może napiszesz algorytm, który realizuje ten proces?