« poprzedni punkt   następny punkt »


12.5. Zasada włączania i wyłączania

Problem, jakim zajmiemy się w tym punkcie wykładu, wydawać się może bardzo prosty, ale takim nie jest.

Niech X1,..., Xn będą zbiorami skończonymi i niech X = X1 ∪ ... ∪ Xn. Jak zależy liczba elementów zbioru X od liczby elementów zbiorów X1,...,Xn?

Rozważmy najpierw sytuację prostą, gdy n=2, tzn. X = X1 ∪ X2, por. rys.12.5.1(a).

Przykład 12.5.1

  1. X1 = {1,2}, X2 = {3,4,5}. Wtedy |X1 ∪ X2| = |{1,2,3,4,5}| = |X1 | + |X2| = 2 + 3 = 5.

  2. X1 = {1,2,3}, X2 = { 2,3,4,5}. Wtedy |X1 ∪ X2| = |{1,2,3,4,5}| = 5 ≠ |X1 | + |X2| = 3 + 4 .

Jeśli zbiory X1, X2 są rozłączne, to |X| = |X1| + |X2|. Jeśli natomiast zbiory X1, X2 nie są rozłączne, to sumując po prostu |X1| + |X2|, elementy należące do przecięcia policzylibyśmy dwa razy. Prowadzi to do konkluzji zawartej w lemacie 12.5.1.

Lemat 12.5.1

Dla dowolnych zbiorów skończonych X1 , X2 , |X1 ∪ X2| = |X1 | + |X2| - |X1 ∩ X2|.

Spróbujemy teraz zbadać przypadek trzech zbiorów.

Przykład 12.5.2

Niech X1 = {0,1,2,3}, X2 = {0,2,3,4,5,6,7,8}, X3 = {0,6,7,8,9}, por. Rys. 12.5.1(b). Jeśli dodamy |X1 | + |X2| + |X3 |, to w tej sumie 2 i 3 zostało policzone 2 razy, bo te elementy występowały zarówno w X1 jak i w X2 . Elementy 6, 7, 8 też zostały policzone dwukrotnie, bo występowały w X2 i X3 . Element 0 występuje we wszystkich trzech zbiorach, więc w sumie policzyliśmy go trzykrotnie. Zatem |X1 ∪ X2 ∪ X3| = |{0,1,2,3}| + |{0,2,3,4,5,6,7,8}|+ |{0,6,7,8,9}| - |{0,2,3}|- |{0,6,7,8}| - |{0}| +|{0}| = 4 + 8 +5 - 3 - 4- 1 + 1 = 10.

Rys. 12.5.1 Obliczamy moc sumy trzech zbiorów.

Lemat 12.5.2

Dla dowolnych zbiorów skończonych X1 , X2 , X3 ,

|X1 ∪ X2 ∪ X3| = |X1 | + |X2| + |X3| - |X1 ∩ X2|- |X1 ∩ X3| -|X2 ∩ X3|+ |X1 ∩ X2 ∩ X3|.

Wzór przedstawiony w lemacie 12.5.2 uogólnia się na dowolną liczbę zbiorów skończonych. Sformułowane niżej twierdzenie 12.5.1 nosi nazwę zasady włączania i wyłączania.

Twierdzenie 12.5.1

Dla dowolnych zbiorów skończonych X1 , X2 , ..., Xn,

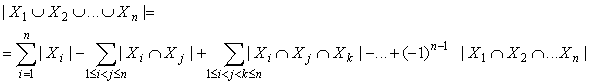
Dowód tego twierdzenia można przeprowadzić przez indukcję, ze względu na liczbę zbiorów n, ale nie będziemy go tutaj prezentować. Zastanówmy się jeszcze tylko nad liczbą składników w tej sumie. Kolejne sumy mają odpowiednio:

  1. n składników, tzn. ,

  2. tyle składników ile jest dwuelementowych podzbiorów zbioru {1,2,...n}, tzn.,

  3. tyle składników ile jest różnych trójelementowych podzbiorów zbioru {1,2,...n}, tzn. itd.

Razem

Zasada włączania - wyłączania, dość niespodziewanie, pomoże nam policzyć liczbę surjekcji, o których była mowa w poprzednim punkcie wykładu.

Twierdzenie 12.5.2

Jeżeli |X| = m i |Y| = n, to liczba wszystkich funkcji całkowitych z X na Y jest równa

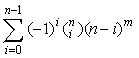
Dowód.

Niech Y={1, ..., n} oraz Ai = {f : X → Y takich, że i ∉ f(X)}. Ai jest wiec zbiorem tych funkcji, które nie przyjmują wartości i, czyli nie są to funkcje na zbiór Y.

Wszystkich funkcji f : X → Y jest n m .Wszystkich funkcji, które nie są "na" jest tyle ile elementów ma zbiór A1 ∪ ... ∪ An. Aby policzyć moc zbioru |A1 ∪ ... ∪ An| zastosujemy zasadę włączania-wyłączania.

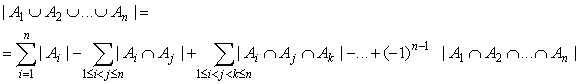
Każdy ze zbiorów Ai jest zbiorem funkcji ze zbioru m elementowego w zbiór (n-1)- elementowy, a zatem |Ai| = (n-1)m. Zbiór Ai ∩ Aj zawiera wszystkie funkcje, które nie mają w zbiorze swoich wartości dwóch elementów i oraz j. Zatem są to funkcje ze zbioru m- elementowego X w zbiór (n-2)-elementowy Y-{i, j}. Jeśli analogicznie przeanalizujemy wszystkie składniki w powyższym wzorze oraz uwzględnimy liczbę składników w całej sumie, to otrzymamy

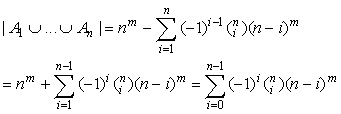
Zadanie 12.5.1 Korzystając z lematu 12.3.1 i z tego, że suma teoriomnogościowa jest działaniem łącznym, udowodnij lemat 12.5.1 .


« poprzedni punkt   następny punkt »