Surjekcje, to jak sobie Czytelnik przypomina, odwzorowania "na". Załóżmy, że f jest funkcją określoną w pewnym skończonym zbiorze X i o wartościach w zbiorze Y, przy czym moc zbioru X jest nie mniejsza niż moc zbioru Y, |Y| ≤ |X|.

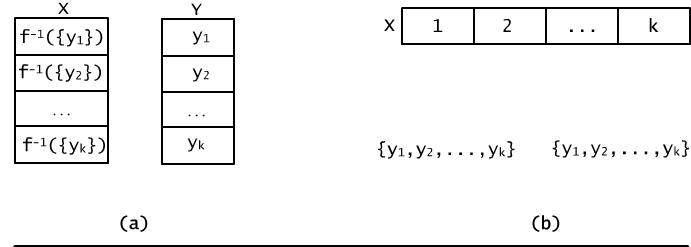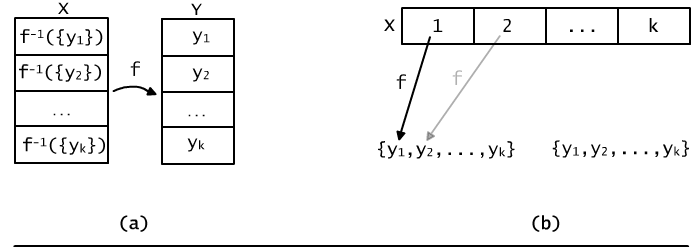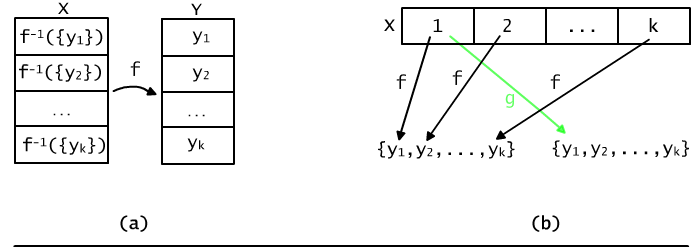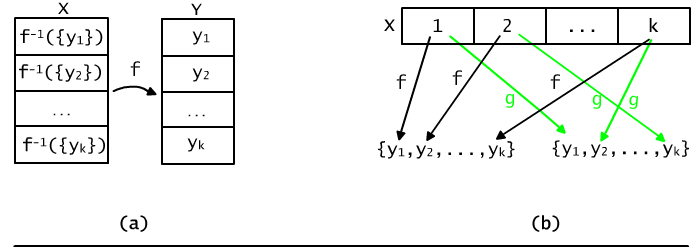
Zauważmy, że jeśli Y = {y₁,y₂,..., y_k} i dana jest jakaś funkcja całkowita f: X → ^na Y, to kładąc X _i = f ^-1({y_i}) dla i = 1, 2, ..., k, otrzymujemy podział zbioru X na k części, Rys. 12.4.1(a).

Rzeczywiście, gdyby zbiory X_i i X_j , dla i ≠ j, miały jakiś element wspólny x, to na mocy definicji przeciwobrazu (por. punkt 4.4) byłoby f(x) = y_i oraz f(x) = y_j, co nie jest możliwe, bo f jest funkcją. Żaden ze zbiorów X_i nie jest pusty, bo każdy element zbioru Y jest wartością funkcji zgodnie z założeniem, że f jest surjekcją. Ponadto, skoro funkcja f jest całkowita, to każdemu elementowi x przypisano wartość w zbiorze Y, np. y_i, ale wtedy x ∈ X_i. Wynika stąd, że suma wszystkich zbiorów X₁,..., X_k to X.

Rys. 12.4.1 (a) Funkcja f wyznacza podział zbioru X. (b) Dany podział zbioru X na k zbiorów wyznacza k! różnych funkcji na zbiór k-elementowy.

Z drugiej strony, jeśli mamy podział zbioru X na k części, X₁,...,X_k to przypisując tym częściom elementy zbioru Y określamy funkcję z X na Y, por. Rys 12.4b. Na przykład, możemy ją określić następująco:

Jest to dobrze określona funkcja całkowita, bo zbiory X₁,..., X_k są zgodnie z definicją podziału parami rozłączne. Element y₁ przypisany wszystkim elementom zbioru X₁ został wybrany dość arbitralnie: równie dobrze mogliśmy wybrać każdy inny element zbioru Y. Mamy zatem dokładnie k! (wszystkie permutacje elementów zbioru Y) różnych funkcji odpowiadających temu samemu podziałowi.

Ponieważ liczba podziałów zbioru X na k części wyraża się liczbą Stirlinga S(n,k), zatem możemy sformułować następujący wniosek:

Pytanie 12.4.1: Na ile sposobów możemy rozdać 5 różnych cukierków trójce dzieci, tak aby każde z nich dostało co najmniej jeden cukierek?

« poprzedni punkt

następny punkt »