Schematem Bernoulliego nazywamy serię n niezależnych powtórzeń tego samego doświadczenia D, dla pewnego n ∈ N. Wykonanie kolejnego doświadczenia D nazywa się próbą. Zajście zdarzenia A nazywa się sukcesem, a zajście zdarzenia A' - porażką.

Jeśli D₁,.... D_n jest ciągiem prób wykonanych w schemacie Bernoulliego, to wyniki kolejnych prób tworzą ciąg, którego wyrazami są zdarzenie A lub zdarzenie A'. Na mocy rozważań w wykładzie 11tym, takich ciągów jest dokładnie 2ⁿ, tzn. tyle ile jest różnych funkcji ze zbioru n-elementowego w zbiór dwuelementowy.

Naturalne pytanie, jakie pojawia się w związku ze schematem doświadczeń Bernoulliego, to jakie jest prawdopodobieństwo, że w serii n doświadczeń sukces zaistnieje k razy. Prawdopodobieństwo to oznacza się przez P(n,k,p). Ponieważ z założenia wynik i-tej próby w schemacie Bernoulliego nie zależy od wyników innych prób, a P(A) = p, zatem prawdopodobieństwo, że w ciągu n-elementowym mieliśmy k sukcesów i n-k porażek wynosi p^kq^n-k. Ponieważ k sukcesów możemy uzyskać na (n nad k) sposobów, bo jest to dokładnie liczba wyborów k-elementowego podzbioru ze zbioru n-elementowego, zatem

Wzór ten nosi nazwę wzoru Bernoulliego lub wzoru dwumianowego, ponieważ wyrażenie występujące po prawej stronie wzoru jest ktym składnikiem w rozwinięciu dwumianu (p+q)ⁿ, zgodnie ze wzorem Newtona.

Przykład 13.6.1

(a) Rozważmy schemat doświadczeń Bernoulliego, w którym rzucamy dziesięć razy symetryczną monetą. Niech sukcesem w tym doświadczeniu będzie wyrzucenie orła O. Ponieważ moneta jest symetryczna więc P(O) = 1/2. Zatem prawdopodobieństwo, że w 10 rzutach monetą uzyskamy 3 razy orła wynosi

(b) Rozważmy doświadczenie A polegające na rzucie symetryczną kostką do gry. Załóżmy, że doświadczenie jest powtarzane 15 razy, a wyrzucenie szóstki będziemy nazywali sukcesem. Zakładamy ponadto, że zdarzenia w tej serii prób są niezależne. Mamy więc do czynienia z doświadczeniem Bernoulliego, w którym P(A)= 1/6 oraz P(A') = 5/6. Zgodnie ze wzorem Bernoulliego prawdopodobieństwo wyrzucenia trzech szóstek wynosi

W zwiazku ze wzorem Bernoulliego powstaje pytanie, jaka jest najbardziej prawdopodobna liczba sukcesów w doświadczeniu złożonym z n prób, w którym prawdopodobieństwo sukcesu wynosi p. Zauważmy najpierw, że

Ułamek po prawej stronie powyższej równości jest większy od jedności wtedy i tylko wtedy, gdy (n+1)p > k, oraz jest mniejszy od 1, gdy (n+1)p < k. Wynika stąd, że

1. dla k<(n+1)p spełniona jest zależność P(n,k,p)>P(n,k-1,p), a
2. dla k>(n+1)p spełniona jest zależność P(n,k,p)<P(n,k-1,p).

Jeśli potraktujemy P(n,k,p) jako funkcję zmiennej k (p jest ustalonym prawdopodobieństwem, a n ustaloną liczbą prób), to dla k < (n+1)p, P(n,k,p) rośnie ze wzrostem k, a dla k> (n+1)p, P(n,k,p) maleje ze wzrostem k.

Rys. 13.6.1 Tabela wartości P(n, k, p) dla różnych wartości p, k i dla n=20.

Na rysunku 13.6.2 przedstawiono wykresy funkcji P(20,k,p) dla różnych wartości prawdopodobieństwa p, a rysunek 13.6.1 przedstawia tabelę wartości funkcji P(n,k,p). Zauważmy, że im prawdopodobieństwo p jest bliższe 0.5 tym wykres funkcji P(20,k,p) staje się bardziej symetryczny.

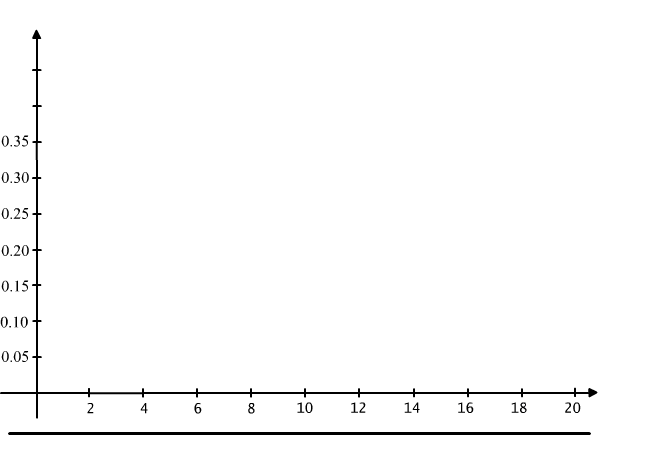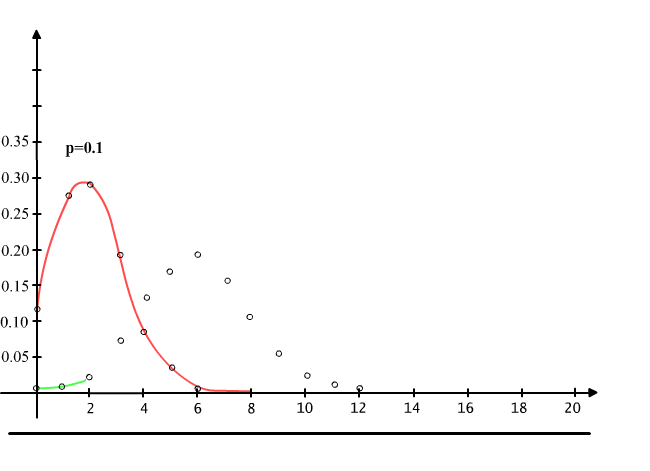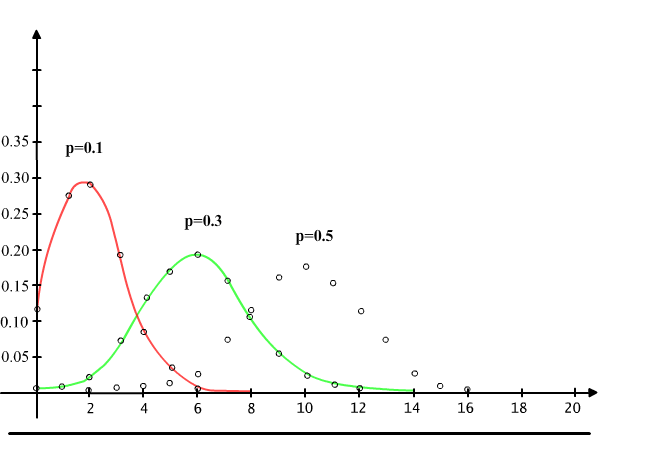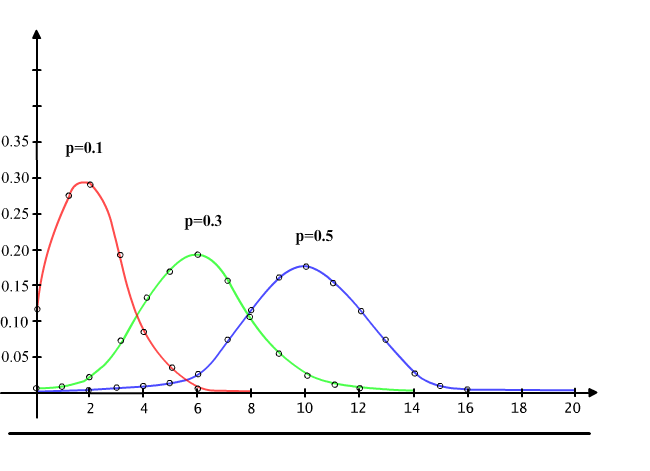
Rys. 13.6.2 Wpływ parametru p na wykres funkcji P(n,k,p) dla n=20.

Jeśli (n+1)p = k (tzn. (n+1)p jest liczbą całkowitą), to mamy P(n,k,p) = P(n-1,k,p) i wtedy najbardziej prawdopodobną liczbą sukcesów w doświadczeniu Bernoulliego z parametrami n i p jest liczba (n+1)p. Jeśli (n+1)p nie jest liczbą całkowitą, to najbardziej prawdopodobna liczba sukcesów należy do przedziału [(n+1)p-1, (n+1)p] i wobec tego, że ten przedział ma długość 1, jest jednoznacznie wyznaczona.

Przykład 13.6.2

Pewien egzamin testowy składa się z 20 pytań, do których podano przykładowe 4 odpowiedzi, ale tylko jedna z nich jest poprawna. Student losowo zaznacza odpowiedzi. Prawdopodobieństwo zaznaczenia dowolnej z odpowiedzi niech wynosi 1/4 dla wszystkich pytań. Załóżmy, że zdarzenia w tym doświadczeniu są niezależne.

(a) Jakie jest prawdopodobieństwo, że student zaznaczy co najmniej 10 poprawnych odpowiedzi?

Aby rozwiązać to zadanie zastosujemy wzór Bernoulliego. Mamy n=20, k=10 i p=1/4. Zatem

(b) Jaka jest najbardziej prawdopodobna liczba dobrych odpowiedzi?

Zgodnie z naszymi rozważaniami, funkcja P(20,k,1/4) jest rosnąca dla k<21/4 oraz malejąca dla k>21/4. Zatem najbardziej prawdopodobna liczba dobrych odpowiedzi na tym egzaminie wynosi 5.

Schemat Bernoulliego odgrywa istotną rolę w teorii rachunku prawdopodobieństwa i w zastosowaniach. Do problemów związanych z tym schematem wrócimy jeszcze kilkakrotnie w związku z omawianymi, w dalszej części wykładu, pojęciami.

Pytanie 13.6.1 Jakie jest prawdopodobieństwo otrzymania w 10 rzutach monetą dokładnie ośmiu orłów?