An ordered pair is a structure <x, y> of two objects x and y, where x is a predecessor of the structure and y is a successor of the structure. Having two arbitrary objects one can construct the ordered pair just by indicating the predecessor and the successor of the pair. For example, Winnie the Pooh and Christopher form the well known (after Milne) ordered pair <Winnie the Pooh, Christopher>

We ought to distinguish the ordered pair from just the pair (Winnie the Pooh, Christopher) that is the two-element set {Winnie the Pooh, Christopher}, in which no element is distinguished by no means. There is no order of elements. On the contrary, in the ordered pair < Winnie the Pooh, Christopher> the order of elements is important: Winnie the Pooh is the first element of the pair (predecessor) and Christopher is the second element of the pair (successor).

In 1921 Kazimierz Kuratowski, gave the successful definition of an ordered pair <x,y> as a set the elements of which are one-element set {x} and two-element set {x,y}.

Such definition of an ordered pair allows to introduce the equality of ordered pairs by saying that two ordered pairs <x, y> and <x', y'> are equal iff the predecessors and the successors of the pairs are identical:

This is in accordance with the equality of sets: if the sets {{x}, {x, y}} and {{x'}, {x', y'}} are equal, then the only possiblity is that {x} = {x'} and {x, y} = {x', y'} or x = x' = y = y'. In the former case we have x = x' and y = y'. As a consequence of the definition, if x ≠ y then

The Cartesian product is named after Rene Descartes (French philosopher and mathematician, 17th century) whose formulation of analytical geometry gave rise to this concept.

Question 2.1.1 Is X × Y = Y × X true for arbitrary sets X and Y?

Example 2.1.1

1. The Euclidean plain we are used to  considering as a set of all points, specified by their vertical and horizontal coordinates that are the real numbers. Thus, Euclidean plain is simply a Cartesian product R × R.
2. The set of all complex numbers C is a Cartesian product R × R. An arbitrary complex number (x + iy) where x and y are real numbers and i is the imaginary unit is nothing else than the ordered pair with the predecessor x and the successor y .
3. When X = {1,2}, a Y = {a,b,c}, then the Cartesian product X × Y consists of the following ordered pairs (1,a), (1,b), (1,c), (2,a), (2,b), (2,c).
4. Let X and Y be intervals in the set of real numbers, for example X = [2, 4] and Y = [3, 6]. Then the elements of the Cartesian product X × Y fill in the rectangle, the projection of which on the axis are the sets X and Y respectively, see Figure 2.1.1.

As the direct consequence of the definition 2.1.1, if one of the considered sets X or Y is empty then the Cartesian product X × Y is also empty, since no ordered pair can be constructed. When both sets X and Y are nonempty then the Cartesian product is nonempty too.

To prove Lemma 2.1.1 it is enough to consider a table (a matrix or an array) with colons indexed by the elements of X and rows indexed by the elements of Y. An element of the product X × Y is then a place in this table. It is obvious that there are n*m places in the table.

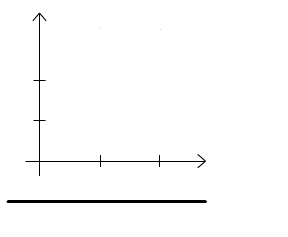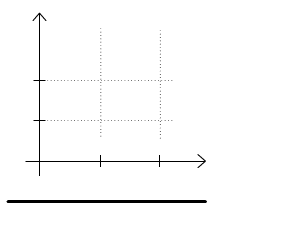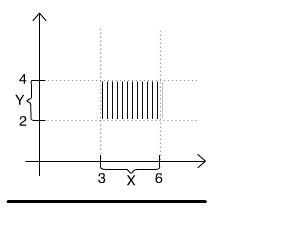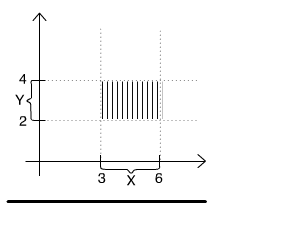
Fig. 2.1.1 Cartesian product of the two intervals X = [2,4] and Y = [3,6].

The main properties of the Cartesian product we shall present in the following lemma.

Properties of that sort can be proved by showing that an ordered pair <x, y> belongs to the left hand side if and only if it belongs to right-hand side of the equation. As an example let us consider the third equation : <x, y> ∈ X × (A\B) iff x ∈ X and y ∈ (A \ B) iff x ∈ X , y ∈ A and y ∉ B iff (x, y) ∈ (X × A) and : (x, y) ∉ (X × B) iff (x, y) ∈ (X × A) \ (X × B).

We will not present the proofs of the other equations. Instead, we will use the graphical illustration to convince the reader of the validity of the second equality, see Fig. 2.1.2. Let X be an interval on the horizontal axis and both sets A and B - intervals on the vertical axis. On the left picture, the intersection of A and B is first constructed and then the product is built. On the right picture, we begin with the products (X × A), (X × B) and then their intersection is constructed. The results are identical in both cases.

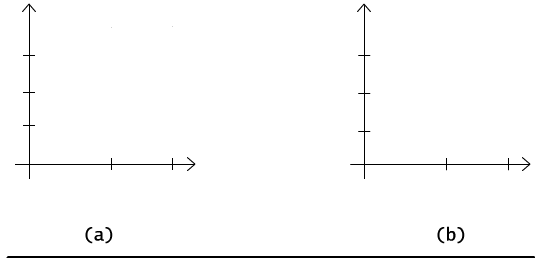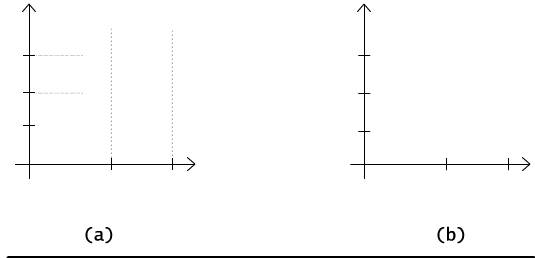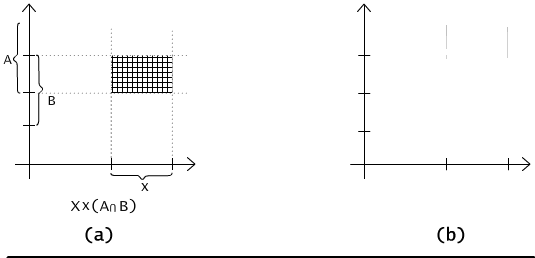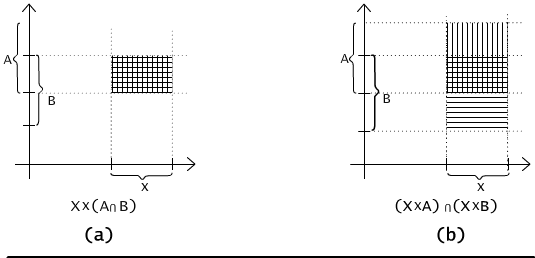
Fig. 2.1.2 Graphical illustration of the equality X × (A ∩ B) = (X × A) ∩ (X × B). 

Question 2.1.2

Try to prove by oneself X × (A ∪ B) = (X × A) ∪ (X × B).

« previous section

next section  »