« previous section    next section »


2.2 The concept of relation

Let X be an arbitrary set. Every subset A of X determines the property W that belongs only to the elements of the set A:

x has a property W iff x ∈ A

Instead of 'x has a property W' we shall write shortly W(x). For example, A = {2i+1: i ∈ N} is a subset of the set of natural numbers, the elements of which distinguishes themselves by beeing odd. The set A determines the property W = "to be odd natural number".

W(x) iff x is odd.

Properties determined by subsets of a set will be called one-argument relations or unary relations.

Consider now the case, when X is a Cartesian product of some sets, for example X = Y × Z. Every subset A of this set consists of the ordered pairs (y, z) such that y ∈ Y i z ∈Z. It determines a property W which refer to ordered pairs :

W(y, z) iff (y, z) ∈ A.

In other words, W determines an interdependence between elements of the sets Y and Z. For example, the subset A of the Cartesian product N × N, A= {(i, j) ∈ N × N : i < j}, determines the property W that belongs to the pair (i, j) iff the second element of the pair (i, j) is greater than the first one.

Definition 2.2.1

Let X and Y be two sets. Any subset r of the Cartesian product X × Y will be called a binary relation (or two-argument relation) in X ×Y. If X = Y, then we say that r is a binary relation in X

If (x, y) ∈ r, then we write x r y and say the relation holds for elements x and y.

Example 2.2.1

  1. Consider all pairs of the form (n, kn), where n and k are integers. This set of pairs is called the divisibility relation in the set of integers and is denoted by |. The pair of integers (x,y) belongs to this relation iff x is a divisor of y, i.e. x | y iff the result of the division of y by x is an integer (x | y is read "x divides y" ).
  2. Let X be a set of some products and R the set of real numbers. In the set of all ordered pairs X × R one can define a binary relation Price_list such that a pair (x, y) ∈ Price_list iff the price of the product x is exactly y.
  3. Let X be a set of cities of Poland. We shall define a binary relation r in X in such a way that (x, y) ∈ r iff there is a direct road that connects the cities x and y.

Definition 2.2.2

The domain of the relation r ⊆ X × Y is a set D(r) consisting of all x ∈ X, for which there is y ∈ Y, such that (x,y) ∈ r, D(r) = {x ∈ X: there is y ∈ Y such that (x,y) ∈ r }.

The co-domain (or range) of the binary relation r ⊆ X × Y is the set D*(r) of all y ∈ Y, such that there is x ∈ X, such that (x,y) ∈ r, D*(r) = {y ∈ Y: there is x ∈ X, such that (x,y) ∈ r }.

Example 2.2.2

  1. Let r = { (1,a), (2, b), (3, c)} then the domain of r is {1, 2, 3} and co-domain {a, b, c}.
  2. Let us define a binary relation r in the set of all real numbers R by:
    (x,y) ∈ r iff x is a square of a real number y.
    The domain of this relation is the set of all not negative reals and co-domain is the set R.
  3. Let A be an arbitrary set. Inclusion, defined on the subsets of the set A, is a binary relation such that its domain and co-domain is a power set P(A).

Binary relations in R we can illustrate geomerically as sets of points on the plane. Such illustration is called a diagram of relation.

Consider the relation r1:

(x,y) ∈ r1 iff y = x2

The diagram of this relation is a set of all points verifying property y = x2, that is a parabola, see Fig. 2.2.1 The domain of r the set of all real numbers and co-domain - the set of all non negative real numbers.

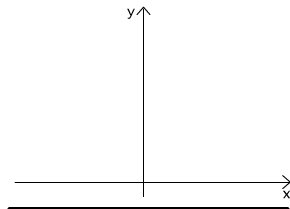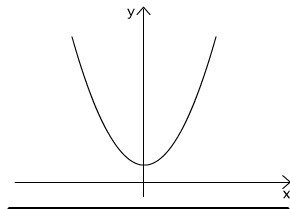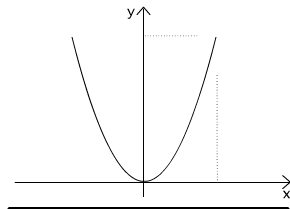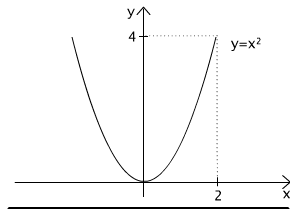
Fig. 2.2.1 Diagram of relation (x,y) ∈ r1 iff y = x2.

Question 2.2.1 Let r be defined in the set of real numbers R as follows (x,y) ∈ r iff x 2 +y 2 = 4. Describe the diagram of this relation. Find domain and co-domain of r.

----- Check the answer -----

Each binary relation defined in the finite Cartesian product X × Y can be represented in the form of a two-dimentional matrix (or table) in which rows are indexed by the elements of X and columns by the elements of Y.

If (x, y) is in the relation then we mark this fact by putting a special sign on the position (x,y), for example 1, true, +. Table defined in this way is called the matrix of the relation.

Example 2.2.3

Let X={1,2,3,4} and Y={5,6,7,8,9}. Then the relation r ⊆ X × Y such that

(x, y) ∈ r iff x is a divisor of y

can be presented as the matrix M(4 × 5) as on the Figure 2.2.2. It has 4 rows and 5 columns denoted respectively by elements of the sets X and Y. The element being on the position (i,j), M(i,j) indicates that the pair (i,j) belongs or does not belong to the relation:

M(i, j) = '+' iff (i, j) ∈ r

In our example (2,6), (2,8), (4,8) etc. are in the relation r, but (2,7) and (2,9) are not and therefore the corresponding cells of the table are not marked.

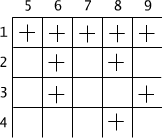
Fig. 2.2.2 The matrix of the relation  (x, y) ∈ r iff x is a diviser of y in the set {1,2,3,4} × {5,6,7,8,9}.

The other way to represent relations are graphs. A graph of a relation is a picture that consists of nodes (or vertex) marked as points on the plane, and egdes, illustrated by arrows that join the nodes. The relation r is represeted in this way in the following sense:

nodes x and y are joined by an arrow going from x to y iff (x, y) ∈ r.

This type of representing binary relations is very useful especially when the domain and co-domain are finite and small sets.

Remark. In what follows, graphs will be the most frequetly used way of representing different notions and therefore we will consider them separately in the section 5 of this lecture.

Example 2.2.4

Consider the relation defined in the example 2.2.3. The diagram of this relation is presented on Fig. 2.2.3(a) and 2.2.3(b). The shape of the nodes and arrows are not essential.

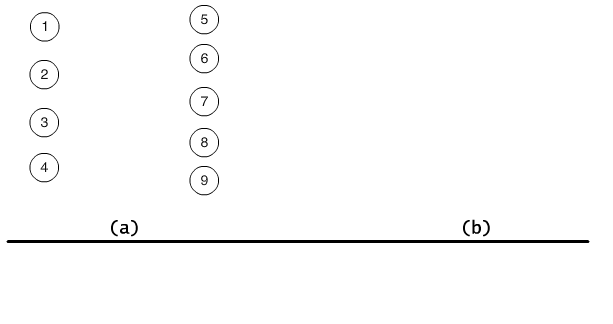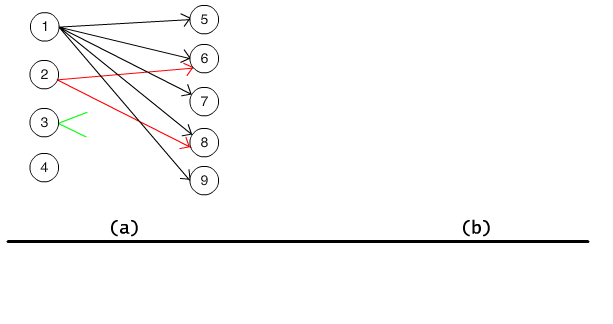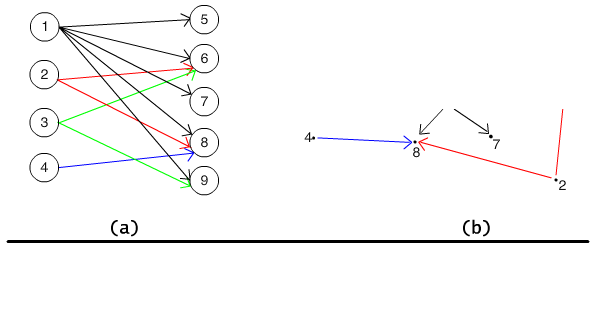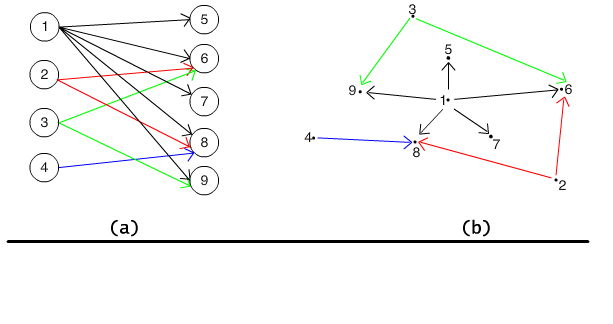
Fig. 2.2.3 Two graphs illustrating the relation r, (x, y) ∈ r iff y is divisible by x.

Question 2.2.2   How many binary relations one can define in the set of five elements ?


« previous section   next section »