The presentation of the notion of graph will be preceded by a short story which is often cited on this occasion. Namely, the Swiss mathematician Leonard Euler, during his time in Konigsberg, had a habbit of going for long walks around the city. The city is located on both banks of river Pregoła and on her two islands, and is spanned by seven bridges, see Figure 2.5.1. Euler tried to find such a tour which would permit him to traverse each bridge one time and go back home. The solution of the problem of Konigsberg bridges appeared in the Euler's paper published in 1736 year, giving the beginning of new branch of mathematics - the theory of graphs. (We will return to the problem of Konigsberg's bridges once again somewhat later.)

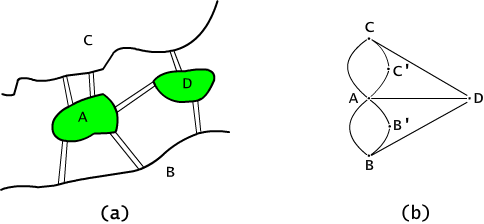
Fig. 2.5.1 (a) Draft of the plan of Konigsberg and  (b) the corresponding graph.

 In this lecture we will talk about simple graphs. They are geomerical shapes built of the points and lines, or arrows joining some of them. We have illustrated relations in this way. The formal definition follows.

Each simple graph determines uniquely the binary relation r in the set of all vertices V,

Conversely, each binary relation r in any set X determines a graph the nodes of which are the elements of the set X and the edges are ordered pairs that belong to r. In general, we will consider the finite graphs, which means that the set of veritices will be finite.

The typical examples of graphs are nets: e.g. the water-supply network, telecommunicational network, etc. Several examples of graphs have already been introduced as illustrations of binary relations. On drawing Fig. 2.5.2 we will introduce one more example: representing the net of road connections. On this example we will explain some basic notions related with graphs.

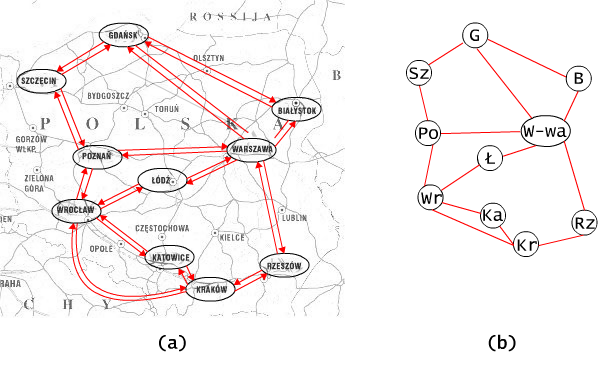
Fig. 2.5.2 A net of road connections.

Please mark, that by the definition of a graph, any two nodes can be connected by one edge at most.

In other words, a path is a route that you travel along edges and through nodes in a graph. All of the vertices and edges in a path are connected to one another. A cycle is a path which begins and ends on the same vertex. The sequence of nodes WR, Ł, W-wa, G,  is a path of the length 3 in the graph presented on picture 2.5.2. On the other hand, the path  W-wa, G, Sz, Po, Wr, Ł, W-wa is a cycle of the length 6.

Question 2.5.1  Is the length of the path equal to the number of vertices of this path?

Example 2.5.1

Let us consider the following algorithm:

in which we have two assignment instructions and one loop. The flow-diagram of this program is presented in Figure 2.5.3. It is a graph with two distinguished nodes "start" and "end". Start-node indicates the state in which no instruction of the program has yet been executed. End-node indicates the state in which all instructions of the program have been executed.  All other nodes contain either an assignment instruction, that ought to be executed at this moment, or a test that must be verified. The arcs show the order in which the actions have to be executed.  Some arcs (i.e. edges of the graph) have words "YES" and "NO" assigned to them. They indicate the way of continuation of the execution, in the case, when the result of the test is positive ("YES") and negative ("NO"). I hope that the Reader will agree that this way of explaining algorithms, agrees with our intuition and helps to understand the structure and the semantics of the program. Having a sequence of values  a[0], a[1], ..., a[n] for some n, one can investigate on this graph each possible execution of the algorithm.   Nota bene: What does this algorithm do?

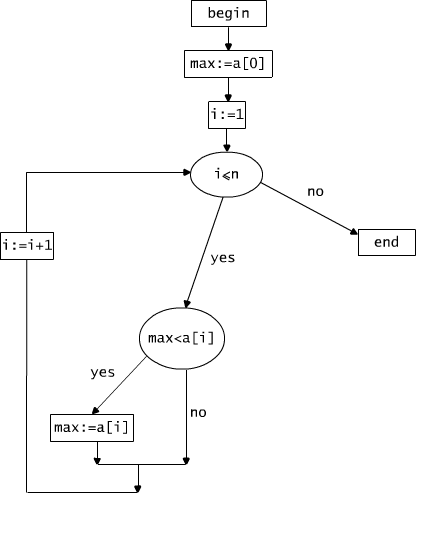
Fig. 2.5.3 Flow-diagramm of a program. 

Question 2.5.2 Present an example of data, for which the realization of the above algorithm corresponds to the path 1,2,3,4,5,7,4,5,7,4, 8. 

Example 2.5.2

Let's assume that you, dear Reader, as a boss of a construction company received an order to build a house. How will you organize this work? At the beginning you will probably establish what actions should be undertaken. Obviously some of them can be executed simultaneously, e.g. by different experts. But some of them have to be executed in the fixed order. For example first we have to build foundations, and later walls.  In general there is a lot of actions. How can we proceed? A simple solution is to draw a graph; see Figure 2.5.4. The nodes of this graph correspond to the actions, and edges will establish in what order one should execute them. This graph will not only permit to embrace the whole of the undertaking at one glance, but also to plan deadlines of beginning and end of individual tasks, to optimize the time and effort.

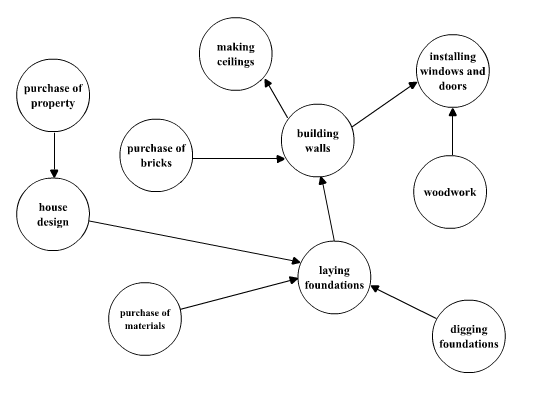
Fig. 2.5.4 The graph of actions during the house construction.

Let's notice that undirected graphs correspond to the symmetric relations. If an edge from v to v' exists then there is an edge from v' to v. The example of such a graph is presented on Fig. 2.5.2 (a). Talking about undirected graphs, we usually simplify drawing just replacing arrows with lines (see Fig. 2.5.2 (b)). Thus, one can consider edges as two - element sets, and not ordered pairs. The notions of path and of cycle in undirected graphs stay the same. The degree of a vertex in an undirected graph is the number of edges that are adjacent to this node. On Fig. 2.5.2 (b), the degree of a node W-wa is 5.

Let’s come back for a moment to the problem of Konigsberg's bridges. One can formulate it as follows: does a path exist in a graph, introduced on the picture Fig. 2.5.1, that is going through all edges of the graph and exactly once by each of them? Is there a cycle through a graph that visits each edge exactly once? Such cycle we call Euler's cycle and such path we call Euler's path. In the case of Konigsberg the answer is negative. Euler formulated the general criterion (necessary and sufficient condition) that characterizes graphs possessing Euler's paths or cycles.

The Euler's criterion, formulated in the theorem 2.5.1, is very simple. When the degree of each node is even, then the graph has an  Euler's cycle and an Euler's path. If there are nodes of odd degree, then either there are exactly two of such nodes and then the graph has Euler's path joining these nodes and has no cycle, or there is no Euler's path in this graph. 

Question 2.5.3

Check, in which of the graphs introduced on Fig. 2.5.5 there exists an Euler's cycle or a path. Remark: if a graph has an Euler's cycle or a path then one can draw it without lifting the pencil from the paper.  Have fun!

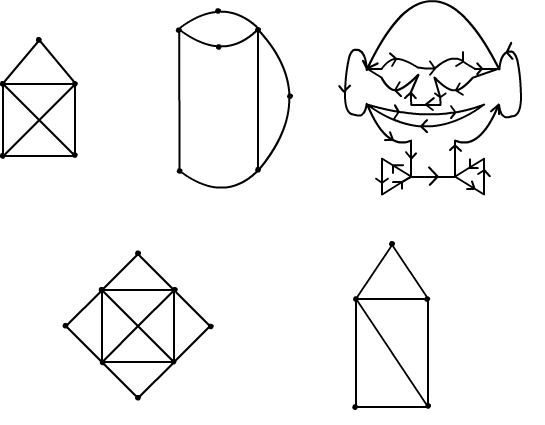
Fig. 2.5.5 Examples of graphs.

Example 2.5.4

Consider a tournament in which 8 teams are playing. Games go in rounds in which teams play in pairs. Only the teams who won in a previous round, proceed to the next round. All games of this tournament can be presented in the form of a graph; see Fig. 2.5.6. The nodes of a graph (numbered from 1 to 8) correspond to the teams taking part in consecutive games (denoted by letters). Edges going out from two nodes x and y meet in a node z only when the teams x,y were playing and z is the vinner.  For example, the game of teams 5 and 6 finished with the victory of team 6. The last round permits to determine out who is the winner of the tournament (Team 6 in our example won).

Fig. 2.5.6  The graph of games in a tournament.

The graph, presented on the figure Fig. 2.5.6 has a particular shape, that is characteristic for some type of graphs. One can observe that this graph has no cycle and any two nodes are connected by only one path.  

Question 2.5.4  What is the smalest number of edges that an undirected connected graph may have?  What is  the maximum number of edges of an acyclic graph?

Remark Each node, with the exception of root, has only one father.

Problem 

Draw your family tree in a way, to make your grandfather a root.

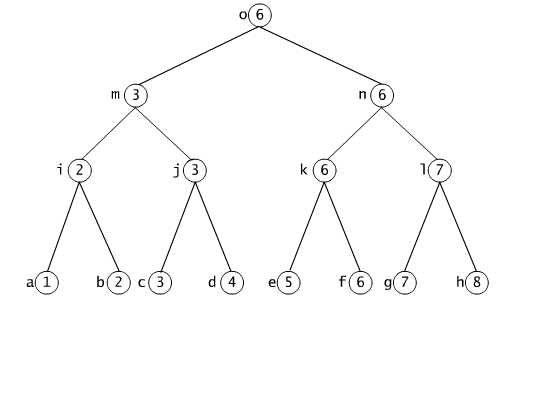
Example 2.5.5

Each arithmethic expression may be pictured in the form of a tree. In such a tree the variables or constants of the expression are leaves, the inner nodes are the executed operations, and the arguments of the operations are edges. In the Fig. 2.5.7 there is a tree representing the expression (x + y) * √ z . On this tree one can clearly see what must be the order of executing the operations. The root of the tree is marked with muliplication since it is the main operation in this expression.

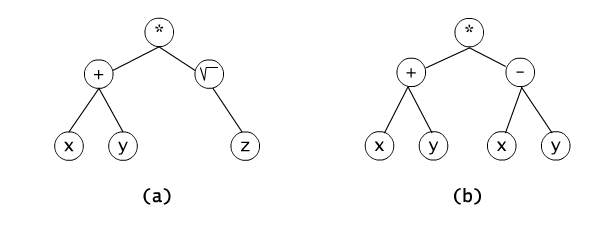
Fig. 2.5.7 The tree on the arithmetic expression (x + y) * √z.

The lenght of the longest path from the root to the leaf is called the height of the tree. If each node of  a tree has at the most two successors, then such a tree is called a binary tree. Since each node in the trees shown in the Fig. 2.5.6 and 2.5.7 has two sons at the most, then those trees are binary. The height of the tournament tree is 3, and the tree form the graph 2.5.7 is 2.

The tree in the Fig. 2.5.8(b) is not binary. It depicts a part of the graph of the possible stuations in the  Shannon game described below (Fig. 2.5.8). The edges of the tree mark possible moves of the players, i.e.  the choices of arcs.

Let's look at a given undirected, connected graph G and its two marked nodes A and B. Two players are making moves in turns. Player 1 in each moves reinforces (by marking with thicker line) on of the edges. Player 2 in each move deletes (by striking trough) one of the not reinforced edges of the graph.

The aim of the player 1 is to build a path connecting the nodes A and B. The aim of the player 2 is to make this task impossible. The player who achieves his gloal first wins the whole game. Have fun.

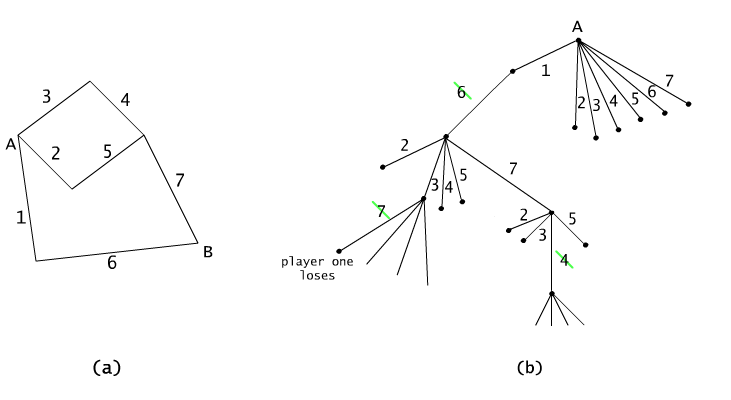
Fig. 2.5.8 Part of the graph of the possible situations in the Shannon game.