| « previous section | next section » |
The set-theoretic operations, like union, intersection and complementation, can be performed on relations treated as sets. If r' and r" are two binary relations in X × Y, then r' ∪ r", r' ∩ r", r' \ r" are subsets of the Cartesian product X × Y too. Thus, they are two-argument relations in X × Y.
If no pair belongs to the relation defined in the product X × Y then we call it empty relation; if all pairs (x,y) for x in X and y in Y are in the relation r, then it is called total relation.
Example 2.4.1
Let r1 = {(x,y) : x < 10, y < 10 and x, y are even numbers} and r2 = {(x,y): x < 10, y < 10 and x, y are odd numbers} be two relations defined in the set of natural numbers less than 10.
(1) The union of r1 and r2 is the relation "to be congruent modulo 2" in the set {0, 1, 2, ..., 9} since it consist of all pairs (x,y) the elements of which are either both odd or both even.
(2) The intersection of r1 and r2 is the empty relation.
(3) The complement of the relation r1 ∪ r2 is the relation that contains all pairs in which one part is an odd digit and the other, an even.
Question 2.4.1 What is the result of the union and the intersection of relations ≤, ≥ defined in the set of natural numbers N?
Definition 2.4.1
Let r be a binary relation in X × Y. The inverse of the relation r, denoted by r-1, is the relation defined in the product Y × X such that for arbitrary x ∈ X and y ∈ Y,
(y, x) ∈ r -1 iff (x, y) ∈ r
Example 2.4.2
(1) The inverse of the relation ≤ in R is the relation ≥ in R.
(2) The inverse of the relation presented on the Fig. 2.4.1(a) is presented on the Fig. 2.4.1(b).
(3) The inverse of the relation {(1,1), (2,4), (3,9), (4,16)} is the relation {(1,1), (4,2), (9,3), (16,4)}.
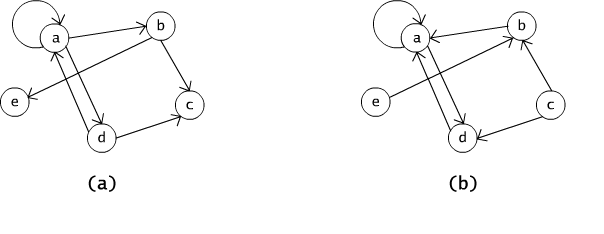
Fig. 2.4.1 En example of a relation (a) and its inverse (b).
Question 2.4.2 Is the equality (r' ∩ r")-1 = r' -1 ∩ r"-1 valid for arbitrary binary relations r', r" in X × Y.
Definition 2.4.2
Let r' ⊆ X × Y and r" ⊆ Y ×Z. By the composition of the relation r' and the relation r" we understand the binary relation, denoted by r' ° r", which is a subset of the set X × Z defined for every x ∈ X and z ∈Z as follows:
(x, z) ∈ r' ° r" iff there is y ∈ Y, such that (x, y) ∈ r' and (y, z) ∈ r".

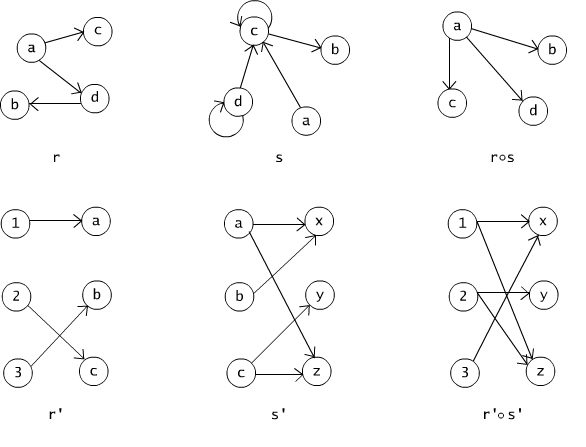
Fig. 2.4.2 Composition of binary relations.
Example 2.4.3
Let r, s, r' and s' be relations illustrated graphically on the Figure 2.4.2(a), (b). The graphs of their compositions r ° s and r' ° s' are presented on the Figure 2.4.2(c).
The next lemma characterizes, in the simple way, the symmetric and transitive relations by means of the operations of composition and of inversion.
Lemma 2.4.1
Let r be a binary relation in X. Then
Proof.
Ad. 1. If r is symmetric and (x, y) ∈ r, then (y, x) ∈ r, and therefore (x, y) ∈ r -1. Conversely, if r ⊆ r -1 and (x, y) ∈ r, then (x, y) ∈ r -1, by the definition of inversion, (y, x) ∈ r. As x and y were arbitrary elements of the set X, it means that r is symmetric.
Ad. 2. If r is transitive and (x, y) ∈ r ° r, then, by the definition of composition, there is z such that (x, z) ∈ r and (z, y) ∈ r. By this and by the transitivity of the relation r, (x, y) ∈ r. Hence r ° r ⊆ r.
Conversely, if r ° r ⊆ r and (x, y) ∈ r and (y, z) ∈ r for some elements x, y, z of the set X, then (x, z) ∈ r ° r. As a consequence we have (x, z) ∈ r, which proves transitivity of r.
Question 2.4.3 Which of the inclusions appearing in the formulation of the above lemma can be replaced by equality leaving the characterization valid?
Problem 2.4.1
Let r' and r" be binary relations in X. Prove that
Question 2.4.4 Are the analogous theorems for the union of relations valid?
| « previous section | next section » |