Functions are special types of relations, so the operations defined on relations can also be applied to functions. Unfortunately not all of them lead from functions to a function.

Let us consider the set-theoretic sum of two functions f and g, f: X → Y and g: U → V.

f ∪ g = { (x,y) : y = f(x) } ∪ {(u,v) : v = g(u)}

If only the sets  X and U are disjoint then the sum f ∪ g is a function, beceuse there is no two pairs who would have the same predecessors and successors. Hence, the sum f ∪ g determines a function h defined conditionally as:

In an opposite case, when  X ∩ U ≠ ∅, the sum f ∪ g does not have to be a function, cf. Fig. 3.3.1. If x ∈ X and x ∈ U, but f(x) ≠ g(x), then both pairs (x,f(x)) i (x,g(x)) belong to the set f ∪ g, and therefore it is not a function.

Fig. 3.3.1 The sum of functions can, but doesn't have to be a function.

In the case of intersection of two functions, f ∩ g, the problem is much easier:

f ∩ g = { (x,y) : y = f(x)} ∩ {(u,v) : v = g(u)},

hence it is a mapping from X ∩ U into Y ∩ V.

Question 3.3.1 The given function  f : X → X is total. When the complement of the set {(x,f(x))}_{x ∈ X} , i.e.  (X × X)/ {(x,f(x))}_{x ∈ X}, is a function?

Let's assume that, our choice of functions is limited to the ones having the real values, so we consider only the  functions f : X → R (the set X does not neccessarily has to be a set of numbers). On such functions we can execute arithmetical operations. Let f₁ : X → R and f₂ : X → R, then one can create the new functions f, g, h in a following manner:

Please note, that the functions f and g are defined for all x, for which also the functions f₁ and f₂ are defined (that is for x ∈ Dom(f₁) ∩ Dom(f₂) ). The function h is defined only for x ∈ Dom(f₁) ∩ Dom(f₂) ∩ {x : f₂ (x) ≠ 0}.

Question 3.3.2 Will the sum of any two one-to-one functions f₁ : R → R i f₂ : R → R, defiened by the formulae (f₁ + f₂ )(x) = f₁(x) + f₂(x), be  a one-to-one function?

Now, we will disscuss the operations of composition  and of inversion. The question then becomes whether the compositon of two functions is a function and whether the inversion of a function is a function as well.  Let f: X → Y and g: Y → V. According to the definition 2.4.2, f ° g is a binary relation defined in a product  X × V. If for some different elements v' and v" of the set V,

(x,v') ∈ f ° g, (x,v") ∈ f ° g

then there would be the elements  y' and y" in Y, such that

x f y' and y' g v' also x f y" and y" g v".

Since f is a function, then it must be y ' = y". In this case however we have y' g v' and y' g v", what contradicts the assumption that g is also a function. From this argumentation we can  conclude that as long as relations taking part in the operation are functions, thier composition is a function as well (por. Fig. 3.3.2). This leads us to the following definition 3.3.1.

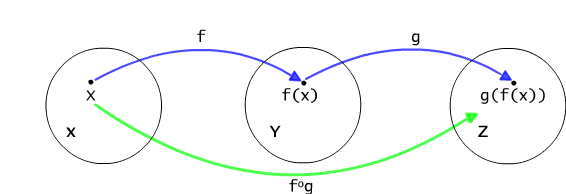
Fig. 3.3.2 Composing functions.

The obvious conclusion of the above is that the composition of total functions is also a total function.

Figure 3.3.3 pictures the exmples of functions and their compositions. The composition of function f(x) = x² +1 with the function g(x) = x+5, defined in the set of real numbers, is function h : R → R such that,

h(x) = (f ° g)(x) = g(f(x)) = g(x² +1) = (x² +1) + 5 = x² +6.

The composition of function g(x) = x+5 with the function f(x) = x² + 1, is function h' : R → R such that

h'(x) = (g ° f)(x) = f(g(x)) = f(x +5) = ((x+5)² +1) = x² +10x +26

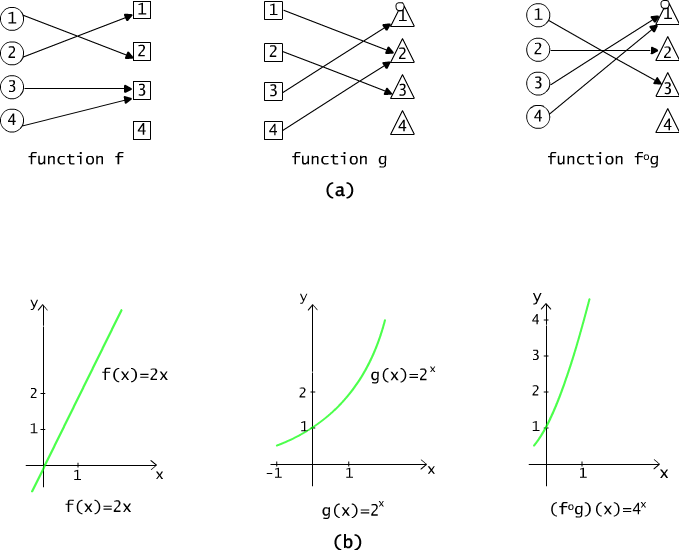
Fig. 3.3.3 Examples of functions and their compositions.

Let's note the observation following from the examples above:

The equation of the point (2) should be understood in a way that the left part of the equation is defined if and only if, the right side is defined, and if both sides have defined values, then they are equal.

The proof  of the above point (1) ensues directly from the example discussed above. For the proof of the point (2) let us notice that assuming that all functions appearing in the equalities below are defined on x, we have 

f ° (g ° h)(x) = (g ° h) (f(x)) = h(g(f(x))) = h((f ° g )(x)). = ((f ° g ) ° h)(x).

Question 3.3.3  Is the composition of two permutations a permutation ?

Proof.

Ad. (1) Let f and g be a one-to-one functions and let x₁ ≠ x₂ . Since f was assumed to be a 1-1 function then f(x₁) ≠ f(x₂). Similarly, function g was also assumed to be a 1-1 mapping, so g(f(x₁)) ≠ g(f(x₂)), hence g(f(x₁)) ≠ g( f(x₂)), that is (f ° g) is a one-to-one function

Ad. (2) Let us take the arbitrary element z₀ ∈ Z. We want to show that for this elemet there is an argument x₀ such that (f ° g)(x₀) = z₀. Indeed, if g is mapping on Z, then there is an element  y₀ in set Y which in transformed in z₀. Similarly function f, as a mapping on the set Y has such element x₀ that f(x₀) = y₀ . Finally (f ° g)(x₀) = g(y₀ )= z₀.

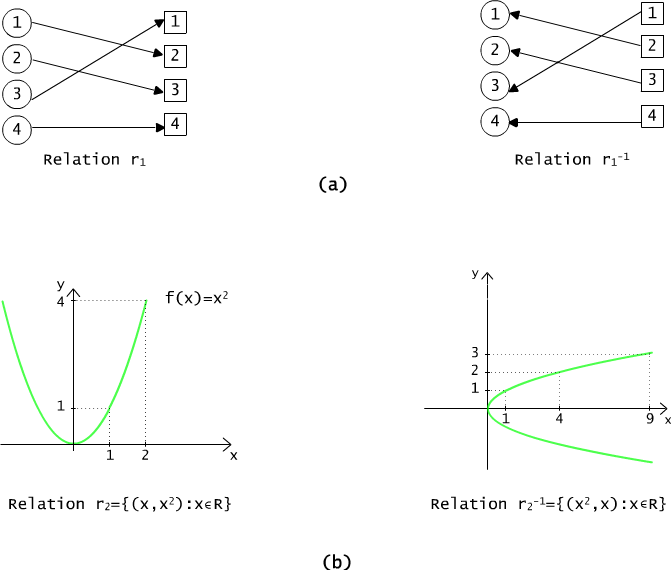
Fig. 3.3.4 The result of inversion does not have to be a function.

Example 3.3.1

(1) Figure 3.3.4 shows two relations r₁ and r₂ and their inverses r₁^-1, r₂^-1. Let us notice that in the first case both relations  r₁ and r₁^-1 are functions. In the second case, even though the relation r₂ is a function, its inverse r₂^-1 is not a function, becase both pairs (4,2) and (4, -2) belong to r₂^-1. What makes such a difference? Namely, the relation r₁ is a one-to-one function and the relation r₂ is not.

(2) Let's consider one more function f : N → NP, f(n) = 2n+1 which maps the set of natural numbers on set of odd numbers NP.  Function g : NP → N determined with a formuleae g(n) = (n-1) div 2 for n ∈ N, is an inverse to f. In fact, g(f(n)) = g(2n+1) = (2n+1 -1) div 2 = 2n div 2 = n.

(3) Exponential function f(x) = 2^x has an inverse called a two based logarithm, denoted usually by lg, lg : R⁺ → R ,

lg x = a     iff    2 ^a = x.

The inverse of a given one-to-one function f is marked just like the inverse relation f ^-1.

Note For every 1-1 function mapping  X on Y there is exactly one inverse function. The inverse of the given 1-1 function is also a 1-1 function.

Question 3.3.4 Let  ~  be a relation in a set of all functions from the set X on X such that f ∼ g wttw f is the inverse of g. Is that a symetrical relation?

Proof.

According to the assumption and the lemma 3.3.2, the composition (f ° g) is a 1-1 function mapping X on Z. Therefore there is an inverse (f ° g) ^-1, which maps Z on X. For any  z ∈ Z and x ∈ X we have

(f ° g) ^-1(z) = x iff (f ° g)(x) = z iff g(f(x)) = z iff there is an y such that y = f(x) i g(y) = z iff there is an y such that f ^-1 (y) = x also g^-1 (z) =y iff f ^-1 (g^-1(z)) = x iff (g ^-1 ° f ^-1)(z) = x.

« previous section

next section »