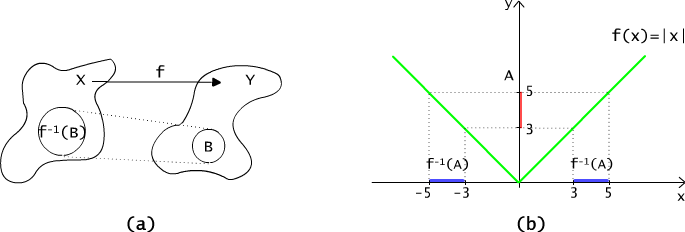
| « previous section |
next section » |
Definition 3.4.1
The image of the set A, A ⊆ X, under the function f : X → Y is a set f(A) of all values of f for those arguments that are in A, (see Fig. 3.4.1(a))
f(A) = {y : there is x ∈ A such that f(x) = y}.
Example 3.4.1
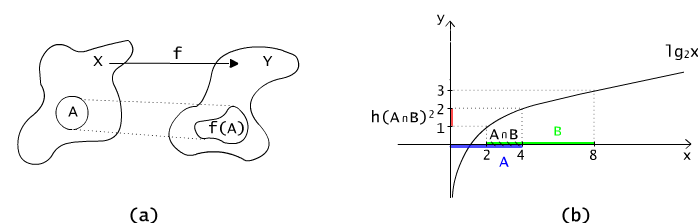
Fig. 3.4.1 The image of a set under a function.
Lemma 3.4.1
For any sets A, B ⊆ X and for any function f : X → Y,
Proof.
Ad 1. First of the equalities is rather obvious:
y ∈ f(A ∪ B) iff y = f(x) for an x ∈ A ∪ B iff x∈ A and y = f(x) or x ∈ B and y =f(x) iff y ∈ f(A) or y ∈ f(B) iff y ∈ f(A) ∪ f(B).
Ad 2. Proof of the second part is analogous. If y ∈ f(A ∩ B), then y = f(x) for an x ∈ A ∩ B. Hence, x ∈ A and x ∈ B and also y = f(x), so y ∈ f(A) and y ∈ f(B) what is equivalent to y ∈ f(A) ∩ f(B).
Let's wonder why in the case of the second formula there is no equality. For that purpose we should analyse the examples once again. For the function g of the example 3.4.1(2), g(A ∩ B) is an empty set, and g(A) ∩ g(B) = {0}. However for the function h of the example (3) we have: A ∩ B = [2, 4], h(A ∩ B) = [1, 2] = (- ∝ , 2] ∩ [1, 3] = [1, 2], compare Fig. 3.4.1(b).
Question 3.4.1 What condition has to be fulfilled by the function f so that f(A ∩ B) = f(A) ∩ f(B) for any sets A and B?
Definition 3.4.2
An inverse image of the set B ⊆ Y under a function f is a set f -1(B) made of those arguments of the function f for which the values belong to B, (compare. Fig. 3.4.2(a) )
f -1(B) = { x ∈ X : f(x) ∈ B}.
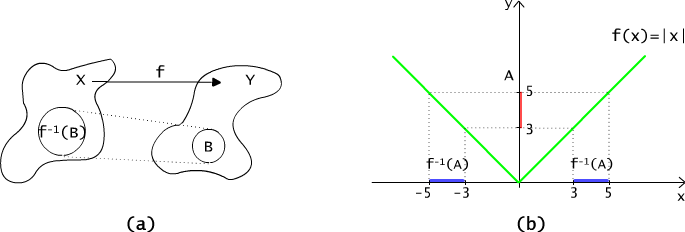
Fig. 3.4.2 Inverse image of set under a function.
The figure 3.4.2 shows the inverse image of the set [3, 5] under function |x|. Inverse images under functions from the example 3.4.1 are noted below:
Lemma 3.4.2
For any sets A,B ⊆ Y and any function f : X → Y,
Proof is very simmilar in both cases. We will exemplify it with the proof of equality (2):
x ∈ f -1 (A ∩ B) iff f(x) ∈ (A ∩ B) wttw f(x) ∈ A and f(x) ∈ B wttw x ∈ f -1(A) and x ∈ f -1(B) wttw x ∈ f -1 (A) ∩ f -1 (B).
Question 3.4.2 Let f : R → R, be a function determined by the formulae f(x) = x 2 -5x + 4. Delimit f(R\R+ ) and f -1 ( {0,4}).
----- Check the answer -----
| « previous section |
next section » |