In this section, we present an application of principle of abstraction to the constructions of integer numbers and of rational numbers.

Example 4.6.1

Let ∼ be the binary relation in the set of pairs of natural numbers  N × N, defined as follows: for every  m, n, k, l ∈ N

(m,n) ∼ (k,l) iff m+l = n+k

The relation ∼ is reflexive, since for every  n, m ∈ N, m+n =n+m (addition is commutative).

The relation  ∼ is symmetric, because, for every pairs (m,n) and (k,l), if (m,n) ∼ (k,l), then m+l = n+k, hence (by commutativity of addition) k+n = m+l, therefore (k,l) ∼ (m,n).

Moreover, the relation  ∼ is transitive, since, if (m,n) ∼ (k,l) and (k,l) ∼ (u,w), then  m+l = n+k and k+w = l+u. Now adding the equalities and applying the associativity of addition, we obtain m + (l + k)+w = n + (k + l)+u, and after reduction we have m+w = n+u, hence (m,n) ∼ (u,w).

All pairs  (m, n), such that the difference m-n is the same belong to the same abstraction class. (c.f. Fig. 4.6.1). The class  [(0, 0)] is the set of pairs with the precedent equal to the succedent, dor example, (1,1), (3,3), (100,100) ∈ [(0,0)]. All the pairs  (m,n) ∈ [(0,0)] share the property m - n = 0. The class  [(1,0)] contains among aothers the pairs (7,6), (4,3), (100,99). The common feature of pairs (m,n) ∈ [(1,0)] is  m-n=1. The abstraction classes of the relation  ∼ determine in this way the integer numbers.

• If m>n, then there exist  k ∈ N such that  n+k=m. The characteristic feature of the class  [(m,n)], where  m>n, is called a positive integer number and is denoted by  +k.

• If m<n, then there exist k ∈ N such that m+k=n. The characteristicfeature of the class [(m,n)], where m<n, is called a negative integer number and is denoted by  -k.

• If m=n, then the class [(m,n)] determines the integer number  0.

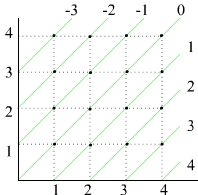
Fig. 4.6.1 Abstraction classes of the equivalence relation defined in the set  N × N (c.f. example 4.6.1).

Question 4.6.1 Let us consider the abstraction classes [(5,8)] and [(1,4)] of the relation defined in the example 4.6.1. Are they equal, [(5,8)] = [(1,4)]?

We are not going to stop at the definition of integer numbers as given in the example 4.6.1. We aim to define operations of addition and of multiplication in a similar way to that applied to natural numbers. If the abstraction classes are to correspond to integer numbers we should be able to execute the arithmetic operations on them. It turns out that on the set of abstraction classes of the relation ~ we can define in a natural way operations + and *. The operations have all properties expected in the set of integer numbers. Below you find the definitions.

for every natural numbers  m, n, k, l.

The symbols used on the rightopposite sides of the above equalities have different meaning (a programmer would say the are overloaded). The symbol + and * occurring on the left side are symbols of defined operations, the symbols + and * occuring on the right sides of equalities are symbols of defining opeartions, they represent the well known operations of addition and multiplication in the set of natural numbers.

Let us check whether in the defined arithmetic of integer numbers:  (+2) + (-3) = -1? The integer  +2 is represented by the class [(2, 0)] which is determined by the pair (2,0) (obviously, it can be represented by pair  (6,4) or (15,13)). The integer numbers -3 and -1 are represented by the classes [(0, 3)] and [(0, 1)]. Hence we have:

(+2) + (-3) = [(2,0)] + [(0,3)] = [(2+0, 0+3)] = [(2,3)] = [(0,1)] = -1.

Remark that the choice of representative of classes has no influence on the result, for example

(+2) + (-3) = [(15,13)] + [(4,7)] = [(15+4, 13+7)] = [(19,20)] = [(0,1)] = -1.

Question 4.6.2 What is the result of multiplication of integers represented by the classes [(5,2)], [(1,4)], i.e. find the value [(5,2)] * [(1,4)]?

Exercise Define the operation of subtraction on the abstraction classes of relation ~ from the example 4.6.1.

Example 4.6.2

Let Z denote the set of integer numbers and let  ∼ be a binary relation defined in the product Z × Z\{0} by the following formula:

(m, n) ∼ (k, l) iff m*l = n*k

Relation ~ is reflexive, since m*n = n*m, therefore (m, n) ∼ (m, n).

Relation ∼ is symmetric, since if (m, n) ∼ (k, l), then m*l = n*k, by the commutativity of multiplication we have k*n = l*m, finally we obtain (k, l) ∼ (m, n), from the definition of ~.

Relation ∼ is transitive. Assume that (m, n) ∼ (k, l) and (k, l) ∼ (u, w), then, by definition, we have m*l = n*k and k*w = l*u. Multiplying the equalities we get m*(l*k)*w = n *(k*l)*u. If k ≠ 0, then (k*l) ≠ 0 ,hence we can divide by (k*l) and obtain  m*w = n *u, therefore (m, n) ∼ (u, v). If k=0, then m*l = 0 and 0 = l*u, these equations imply (recall that l ∈ Z\{0}) that m= u = 0 from the definition we get (m, n) ∼ (u, v).

In this way we proved that ∼ is an equivalence relation.

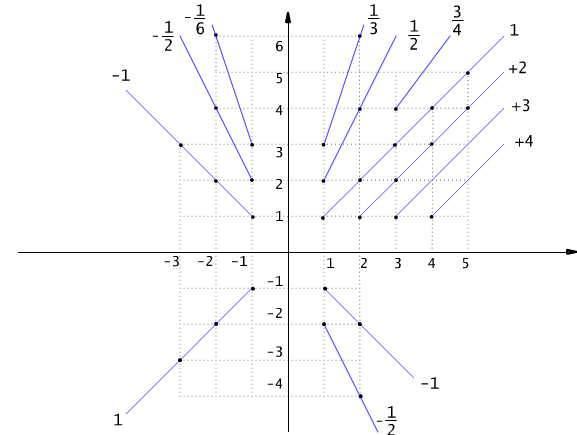
Fig. 4.6.2 Abstraction classes of equivalence relation ~ defined in the product Z × Z\{0} (cf. example 4.6.2).

Let us remark that all pairs  (m,n) which belong to the same abstraction class share the same value of guotient  m/n (cf. Fig. 4.4.1). For example the pairs (2,4), (3,6), (5,10), (15,30) are inthe relation and belong to the class [(1,2)]. Let us associate the rational number 1/2 to this class. In general, abstraction class  [(m,n)] determines the rational number  m/n.

As in the preceding example, we are able to define arithmetic operations on abstraction classes corresponding to the operations on rational numbers. We define

for every integer numbers m, k ∈ Z and n, l ∈ Z\{0}.

Operation + i * which appear on the left sides of the above definitions are defined by means of corresponding operations in the set Z of integer numbers. One can prove that all the laws of the arithmetic of rational numbers are satisfied by the operations on abstraction classes.

Question 4.6.3 Evaluate the expression [(3,4)] + [(1,8)].

Example 4.6.3

Let R^{+ N} denote the set of all functions f: N → R⁺ and let  ∼ be a binary relation in this set such that for every function  f, g ∈ R^{+ N},

f ∼ g iff there exist positive real numbers  c₁, c₂, n₀, such that g(n) ≤c₁f(n) and c₂f(n) ≤g(n) for all  n > n₀.

Relation ∼ is an equivalence relation. Reflexivity and symmetry follow directly from the definition. We shall prove the transitivity property. Assume that f ∼ g and g ∼ h. Then there exist positive constants c₁, c₂, n₀ and c₁', c₂', n₀' such that the following inequalities hold

This implies that for every natural number n greater than both numbers  n_{0 ,} n₀' the following inequalities hold

This means that f ∼ h.

An abstraction class [f], determined by a function f is usually denoted by  Θ(f). Functions n + lg n + n², 2n+(n+7) ²+100, (n⁵ + 3)/(n³-1), 2 ^{2lg n} belong to the same abstraction class of relation  ∼ , namely to  [n²]. Observe that each of the following functions lg n, n, nlgn, n², n³, 2ⁿ, 3ⁿ , nⁿ belong to a different abstraction class.

When  f ∼ g  we say that functions  f and g are of the same order (cf. section 3.6).

Question 4.6.4 Consider the relation "to be of  the same order" from the example 4.6.3. Verify the validity of the following formulas:

(a) sqrt(n) + lg n  ∼  lg n
(b) 2n + 2 ^{2lg n}+100  ∼ 3 n²
(c) 2_ⁿ + 3_ⁿ  ∼ 4_ⁿ

« previous section

next section »