In the present lecture we shall use the symbol ≤ to denote an ordering relation. The set X in which the ordering relation is defined will be called ordered set and will be denoted by <X, ≤ >. To stress the fact that two elements x and y are in the relation ≤ and that they differ, we shall use the notation x ≤ y. In a similar manner we use the relation ≤ in the set of real numbers R.

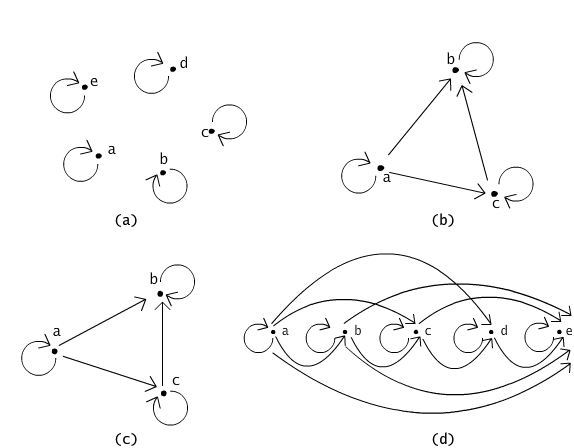
Fig. 5.1.1 Examples of partially ordered sets.

In the Figure  5.1.1 we present the examples of graphs illustrating ordered sets. The graph of Figure  5.1.1(a) shows a partial ordering. This relation is obviously reflexive. It does not hold for any pair of different elements and therefore the predecessors of implications (2) and (3) are not satisfied. As a consequence, the relation is antisymmetric and transitive too. The graph of Figure 5.1.1(b) illustrates also an ordering relation. Contrary to the former relation, in this case for certain distinct elements the relation is established: a ≤ b and a ≤ c. The relation illustrated on Figure 5.1.1(c) allows to sequence all elements in a row a ≤ c ≤ b. Similarly as in Figure 5.1.1(d), where any two elements are comparable by the ordering relation.

Question 5.1.1  Is a complete graph an illustration of an ordered set?

Example 5.1.1

1. As the first example let us consider the relation ≤ in the set of real numbers.It is evident that for every real numbers x, y, z ∈ R, we have x ≤ x, if x ≤ y and y ≤ x, then x = y, if x ≤ y and y ≤ z, then x ≤ z. As a consequence, we obtain that the sets N of natural numbers, Q of rational numbers and Z of integer numbers are also ordered by the relation ≤.
   
   
2. The relation  ≤ defined in the set R^R of all functions from the set R into R and such that for  f, g ∈ R^R

   f ≤ g iff for every  x ∈ R, f(x) ≤ g(x),

   is an ordering relation in the set  R^R. Indeed, for every x ∈ R holds f(x) ≤ f(x)  i.e. the relation ≤ is reflexive. Let  f ≤ g and g ≤ f and let x be a fixed real number. By the first assumption,  f(x) ≤ g(x) and g(x) ≤ f(x) by the second assumption, hence by antisymmetry of the relation  ≤ we obtain  f(x)=g(x). This reasoning can be repeated for any  x ∈ R, proving in this way that for every  x ∈ R, f(x) = g(x). Hence f = g.
   In order to prove the transitivity of the relation  ≤ let us suppose that  f ≤ g and g ≤ h. Consider an arbitrary real number x. According to the assumptions, we have f(x) ≤ g(x) and g(x) ≤ h(x). We now use the transitivity of the relation  ≤ , and obtain f(x) ≤ h(x). Since x was an arbitrary real number, we conclude that f ≤ h. Hence, the relation  ≤  is transitive, which ends the proof that  ≤  is an ordering relation.
   
   
3. The relation illustrated in the previous example uses in an essential way the properties of the relation  ≤ in the set of real numbers. It may seem that an appearance of the relation  ≤ in a definition of a new relataion garantees that the newly defined relation is an ordering relation. It is not true, however, as it is shown by the following counter-example. Let us consider the relation r defined in the set of functions R^+N, such that

   f r g iff there exist positive constants  c and n₀, such that f(n) ≤ c*g(n) for n > n₀.

   According to our definition, two functions f and g are in relation r, if f = O(g), i.e. the function f grows much more slowly than g (c.f. section  3.6). The relation r defined in this way is reflexive and transitive, it is not antisymmetric however. Let  f(n) = 2n and g(n) = 5n. Then for every n we have f(n) ≤ g(n) and for every n ∈ N, g(n) ≤  f(n). Hence  f = O(g) and g = O(f), but obviously the functions f and g are not equal (f ≠ g).

Question 5.1.2 Is the relation < of "being less" an ordering relation in the set R of real numbers?

« previous section

next section »